[文献阅读]侵蚀攻击：利用侵蚀改善对抗样本可迁移性-ErosionAtt

Information

论文位置：[10.1109/TIP.2023.3251719] Erosion Attack: Harnessing Corruption To Improve Adversarial Examples

日期：2023-04

关键词：Adversarial Attack, Optimization, Computational modeling, Perturbation methods, Neural networks, Training, Closed box, Data models

出处：IEEE Trans. on Image Process.

摘要

本论文提出了一种新颖的可迁移对抗攻击，突出其安全局限性。

本论文确定了当前攻击可能失败的两个内在原因，并提出对应的解决方法：

• 数据依赖：提出了数据侵蚀(Data Erosion)方法。其涉及到寻找在简单原始模型(vanilla models)和防御模型中共有的相似性为，以帮助攻击者以更高的机会欺骗鲁棒模型
• 网络过拟合：克服网络过拟合困境：将单一的代理模型扩展到具有高度多样性的集成结构，从而产生更多课前一的对抗样本

背景

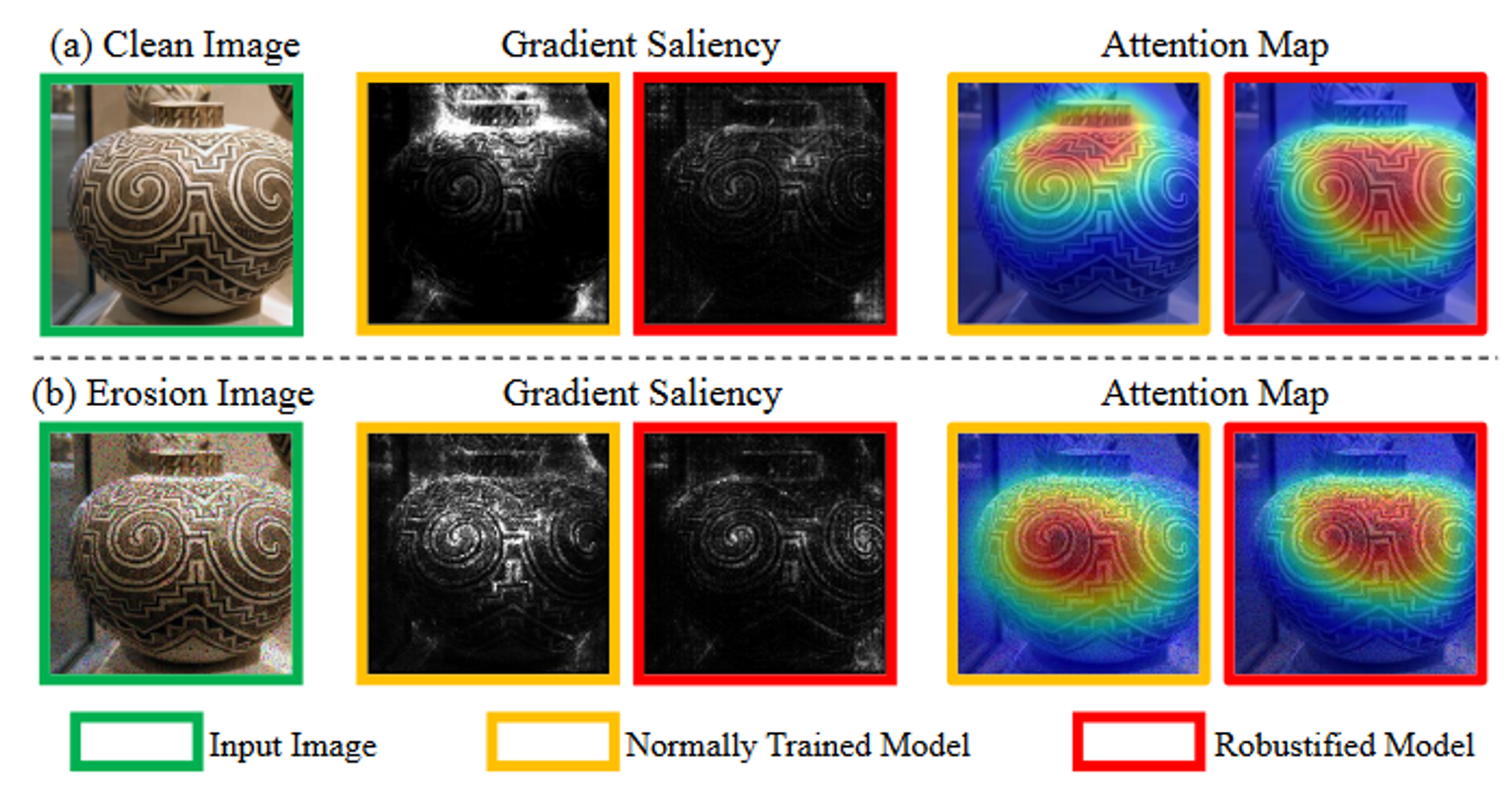
利用现成的代理模型生成对抗样本来欺骗远程黑盒模型是一种更具威胁性的方式，即可迁移对抗攻击。

当前可迁移攻击方法在防御场景中效果较差的两个重要原因：

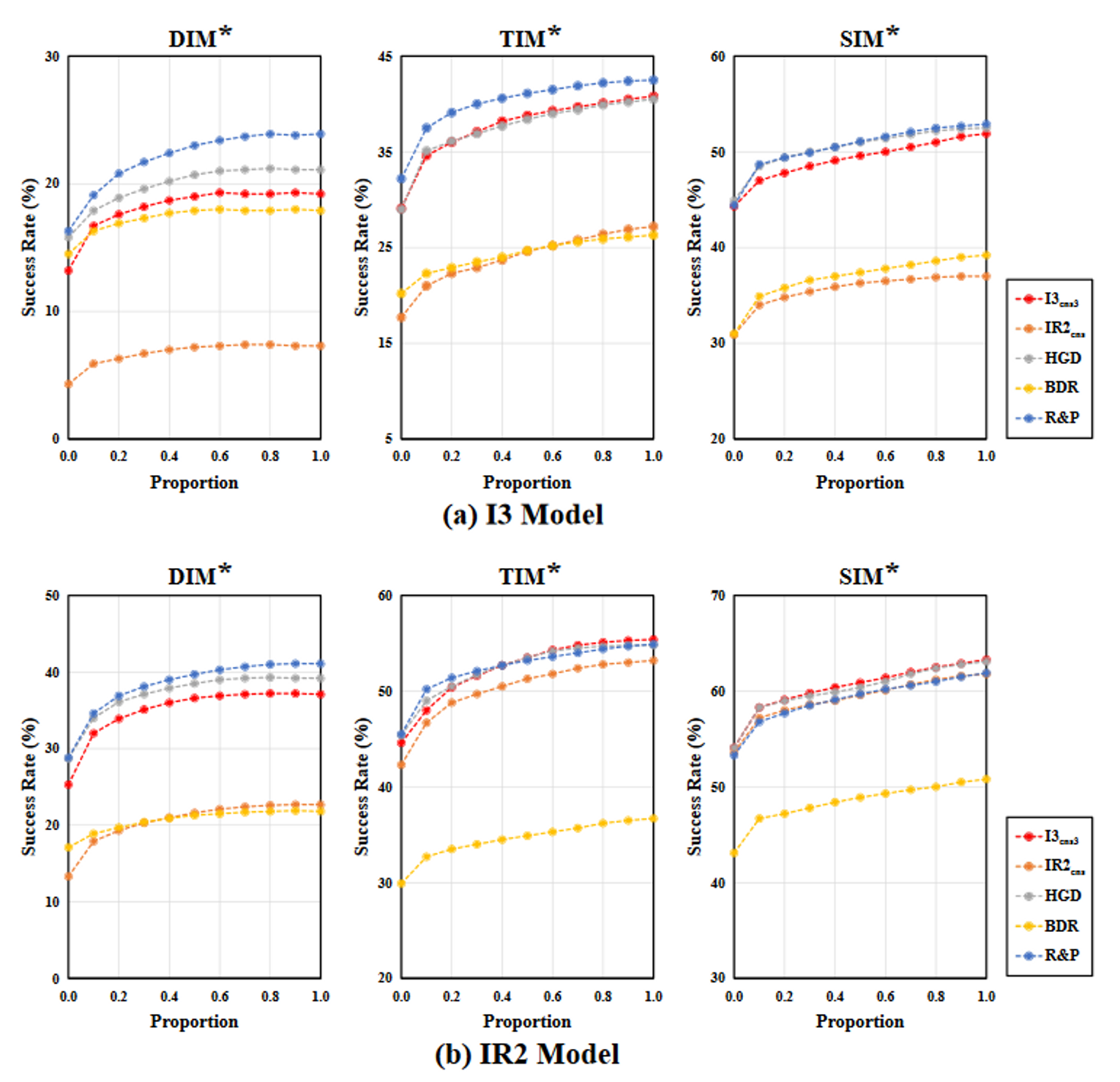
• 数据依赖：对抗样本与输入数据高度相关，如果输入数据是干净图像，防御模型通常与正常训练的模型表现不同，如图1(a)所示。这可能会简介影响对抗样本的可迁移性，因为大多数方法只考虑干净图像并在正常训练的模型上进行优化。——大多数对抗样本可以很好迁移到其他vanilla models而不能攻击防御模型：为此而寻找一种共有的相似特征的特殊增强源，如梯度注意区域；通过在攻击过程中融入上述增强数据，对抗样本对原始数据的依赖程度降低，从而产生更高的可迁移性来欺骗黑盒防御。
• 网络过拟合：降低对抗样本与代理模型之间的耦合性是一种自然选择。集成攻击：在优化过程中采用多个网络，以减少对单个模型的依赖。本论文提出的EA方法为了克服集成攻击的物理限制和特征级攻击由于池化等特定网络组件而丢失有价值信息的弱点，通过利用中间特征，对抗样本从不同的决策边界中学习，将单个模型拓展到损坏的网络，以低成本实现集成攻击。

数据侵蚀可以看成一种产生良好样本的数据增强技术，网络侵蚀通过构建多样化的集成来实现模型增强。

方法

目标

设计一个鲁棒通用的可迁移攻击框架来欺骗不同的防御模型，并揭示当前模型的潜在不安全性。

• 数据侵蚀方法：人工损坏的图像不仅表现出与干净图像不同的梯度显著性和热图，而且在vallina模型和防御模型之间表现出更小的差异。因此将这些侵蚀图像作为良好的增强数据加入到攻击中来更新扰动。
• 网络侵蚀方法：大多数基于梯度的攻击只考虑最终的预测分布来计算梯度，忽略了一些前向传播操作造成的有价值的特征丢失，为了学习各种分类边界并以较小的代价收集丰富的中间表示信息，简单修改现有模型的结构来创建一个损坏的网络用以实现集成化，以避免网络的过拟合。

数据侵蚀

在优化中对图像进行侵蚀以产生侵蚀增强数据，作为新的攻击目标函数：

$\arg\max\limits{x’}{J(x’,y)+\sum\limits{i=1}^nJ(x_{e_i}’,y)}$，(1)

其中：

• $x_{e_i}’$是侵蚀图像，由每一步侵蚀当前$x$产生的
• $n$是采样数
• $L∞-norm$，即$||x-x’||∞<\epsilon$

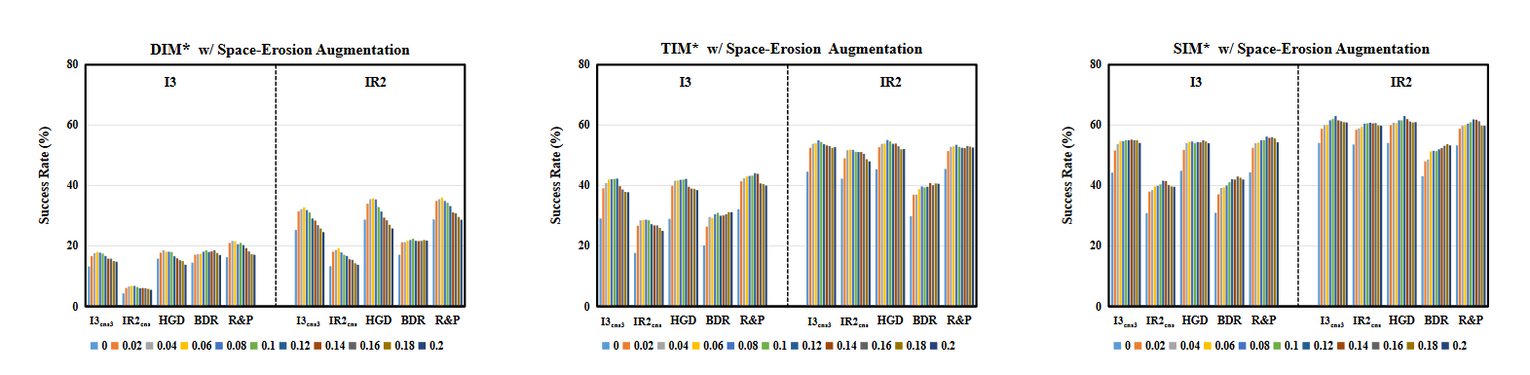
实验发现，性能最好的增强数据是由随机破坏输入图像像素连续性的空间侵蚀策略产生。除此之外的颜色侵蚀和亮度侵蚀较差。

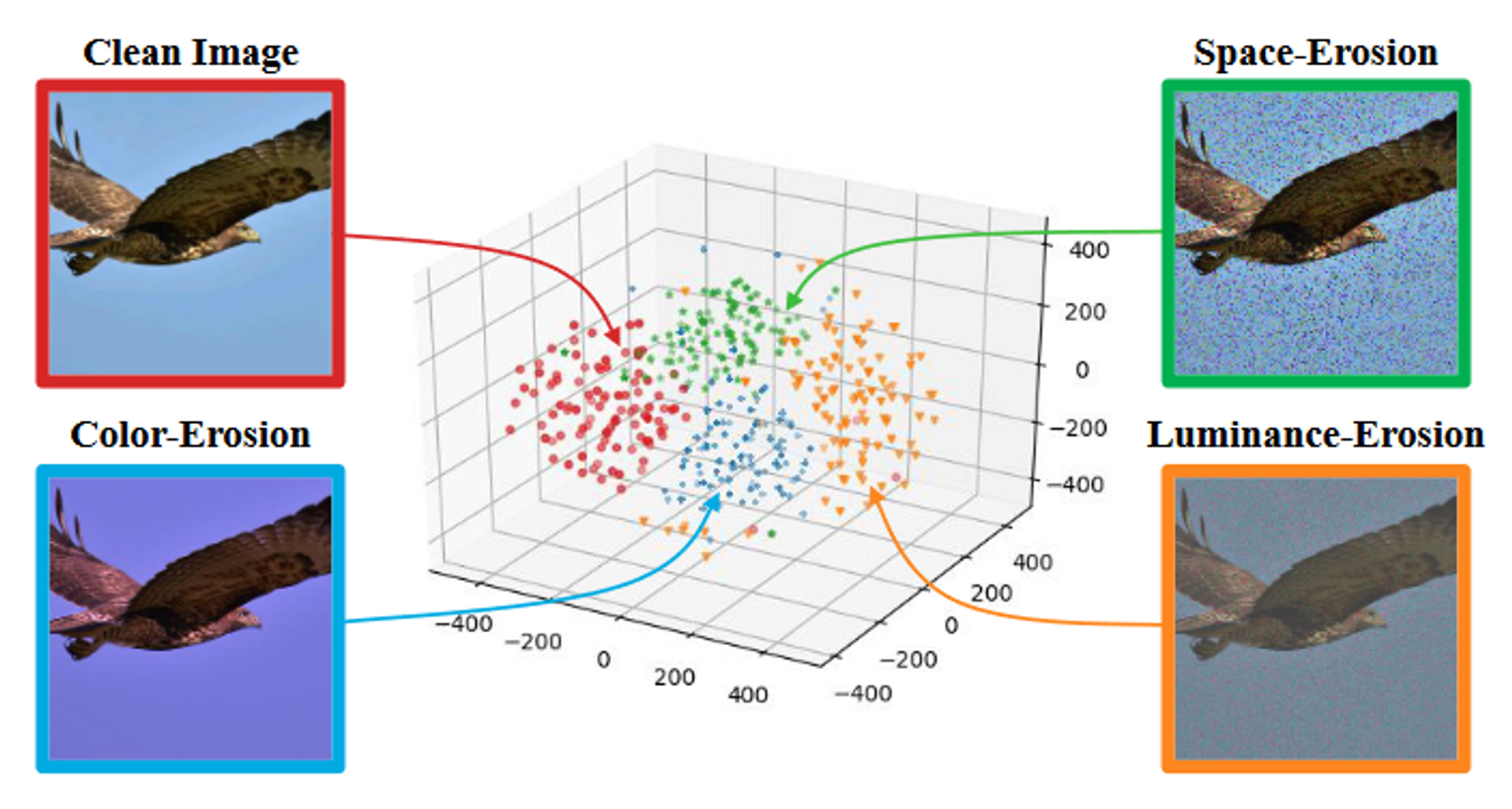
空间侵蚀

如果图像中出现的额相邻像素的空间连续性已经破坏，正常的训练模型可能会改变其判别区域，更多关注结构和一般特征而不是局部细节，类似于鲁棒模型行为。这启发我们破坏当前图像$x’$的空间连续性来采样侵蚀数据$x’_e$：

$x’_e=M\cdot x’,\ M\sim Bernulli(1-ξ)$，(2)

其中：

• $M$是在每次迭代中随机生成的二进制掩码
• $ξ$是一个预定义的概率以控制侵蚀水平；若$ξ=0$，则没有像素被破坏，若$ξ=1$，则所有元素值被破坏为0.

空间侵蚀类似于对输入数据应用dropout操作，区别在于空间侵蚀没有将剩余的像素放大$1/(1-ξ)$

色彩侵蚀

彩色损毁图像具有与空间损毁数据类似的性质。通过随即线性组合基本彩色图像生成侵蚀图像：

$xe’=\alpha_1\cdot x’{gb}+\alpha_2\cdot x’{rg}+\alpha_e\cdot x’{rb}$，(3)

其中：

• $x’{gb},x’{rg},x’{rb}$（即如：$x’{gb}$保持g和b而破坏r）为对抗样本$x’$的基本彩色图像
• $\hat{\alpha}_i$为取自均匀分布$U(0,1)$的正权重$\alpha_i=\hat{\alpha}_i/\sum_j\hat{\alpha}_j$

亮度侵蚀

首先将输入图像从RGB换到YUV空间，然后对Y(亮度)和V(饱和度)通道中的分量进行随机扰动： $x_e’=\gamma_1\cdot x_y’+\gamma_2\cdot x’_v,\ \gamma_i\sim\mathcal{N}(I,\sigma_e^2)$，(3)

其中：

• $x_y’,x_u’,x_v’$表示基本亮度图像（即如：$x_y’$从$x’$保留Y通道的分量）

差异

以往的方法在攻击中也是用增强，与本论文的主要差别：

1. 其采用增广来避免局部极大值，而本论文的增广数据是用来缩小正常模型和防御模型之间的差距
2. 其选择保持损失的变换来保持图像细节和实现模型增强，而本论文不属于这种类型操作，而是迫使模型通过侵蚀像素来关注一般特征。

网络侵蚀

为了通过利用中间特征来学习不同的决策边界，我们攻击原始网络即破坏其损坏版本的和集成，以较小代价生成更具威胁性的对抗样本如图3(a)。目标函数为：

$\arg\max\limits_{x’}={J(x’,y)+J_e(x’,y)}$，(4)

其中$J_e$为已构建的侵蚀网络的目标函数。

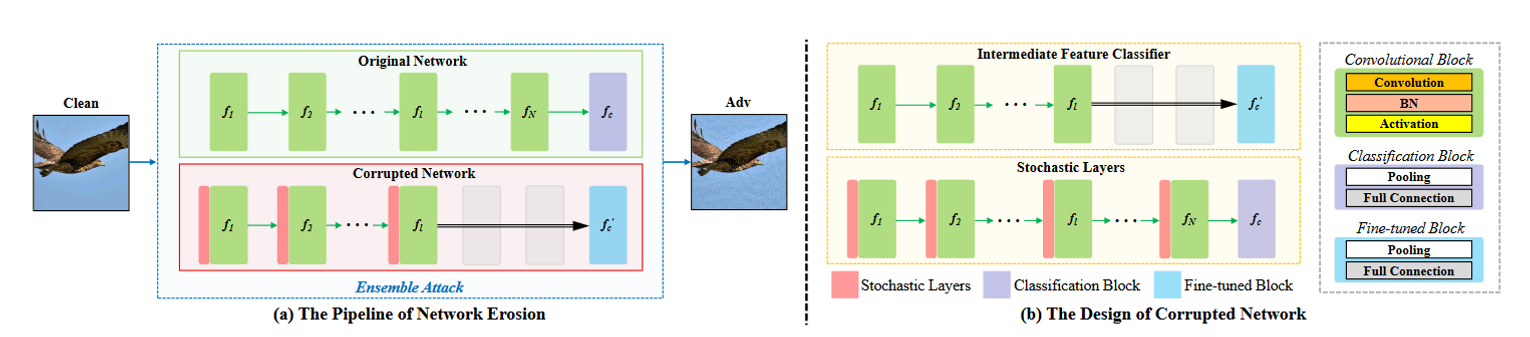
如图3(b)所示，原始网络与损坏网络的主要区别在于：

1. 通过少量的微调开销，破坏了原始模型的结构，构建了一个具有不同边界的中间特征分类器
2. 在卷积块钱加入随即层，进一步提高模型的多样性和鲁棒性

中间特征分类器

假设被攻击对象有一部分图像可以被代理模型正确标记，即使这些图像不属于代理网络和黑盒网络的训练集，也是合理的。为此我们旨在用较小的代价提取这些图像的表示，用于微调中间特征分类器（IFC）。特别的，对于给定图像$x$，我们可以从一个代理模型$f$得到它在第$l$层的预测标签$y$和中间特征$z_l$，即$y=f(x),\ z_l=f_l(x)$，因此，利用标准交叉熵损失(CE)在校的替代数据集$\mathcal D’$上训练特征分类头$f’_e$：

$\begin{split}J_{CE}(x,\theta’)=\mathbb{E}{x\sim\mathcal{D}’}[-y^T\log f_c’(z_l)]\ =\mathbb{E}{x\sim\mathcal{D}’}[-f(x)^T\log f_c’(f_l(x))]\end{split}$，(5)

其中$f’_c$是IFC的微调块，与白盒模型$f$的分类头$f_c$具有相同结构。

直觉上IFC的结构可以看作是特定的中间层微调后的分类块之间建立跳跃链接， 而跳跃的层已经“损坏”而无法工作

随机层

在整个网络的每个卷积块之前嵌入随机层，是的当前图像通过层时，特征具有多样性，这使得在保持高分类精度的同时，输出概率的多样性变大。设计了三个不同的随机层：

• 随机缩放层。在训练阶段，直接在图层中加入高斯噪声以提高训练模型的鲁棒性。提出将特征在小范围内进行缩放：

  $z_{l+1}=g_l^\mathfrak{r}(z_l)=s\cdot z_l,\ s\sim\mathcal{N}(I,\sigma^2)$，(6)

  其中：

  • $g_l^\mathfrak{r}$是第$l$层的随机缩放操作
  • $z_l+1$是下一层的特征图
  • $s$是从$x_l$的同一维空间中采样的向量
  • $\sigma=0.025$

• 特征平滑层。扰动在像素级较小，在特征空间逐渐增大，即噪声随着图像在网络中传播而被激活。引入高斯核对特征进行平滑，提高待攻击模型的鲁棒性：

  $z_{l+1}=g_l^\mathfrak{f}(z_l)=W_d*z_l$，(7)

  其中：

  • $g_l^\mathfrak{f}(\cdot)$表示特征平滑操作
  • $W_d$是核为$3\times 3$大小的归一化高斯滤波器，用于实现与特征图$z_l$的卷积操作

• 级联组层。将提出的两个层集成到单个模块中：

  $z_{l+1}=g_l^\mathfrak{s}(z_l)=g_l^\mathfrak{r}\circ g_l^\mathfrak{f}(z_l)$，(8)

  其中定义符号$\circ$为复合函数，即：$g_l^\mathfrak{r}\circ g_l^\mathfrak{f}(z_l))$

EA框架

数据服饰引入了不同注意力区域的良好增强，以缓解数据依赖效应。网络侵蚀产生了具有多样化决策边界的损坏网路，以防止网络过拟合效应。将之结合到一个通用框架中，进一步增强对抗攻击的可迁移性。

当前的可迁移攻击可以自然地集成到所提出的侵蚀攻击框架中，以生成更强的对抗样本。如EA-TIM的集成版本只需要更新算法中的第10行：

$g=W*\nabla_x\tilde{J}$，(9)

同理于DIM、SIM组合版本生成EA-DIM和EA-SIM。

实验

实验设置

• 归一化像素中最大扰动$\epsilon=0.05$
• 总迭代次数$T=10$
• 步长$\alpha=0.005$
• 对于baseline，动量衰减$\mu=1.0$
  • DIM的转换概率$p=0.7$
  • TIM的高斯核大小为$11\times11$
  • SIM的缩放图像数量$m=4$
  • SGM的跳跃衰减$\gamma=0.2$
  • VT的方差调整$\beta=1.5，N=20$
  • LAFEAT使用其提出的DLR损失结合倒数第二个训练的logits层
  • FIA为Incv3、Incv4、IncRev2和Rev50分别选择了最优层，即$Mixed_5、Mixed_6f、Conv_4a、block2_unit6$

实验分析

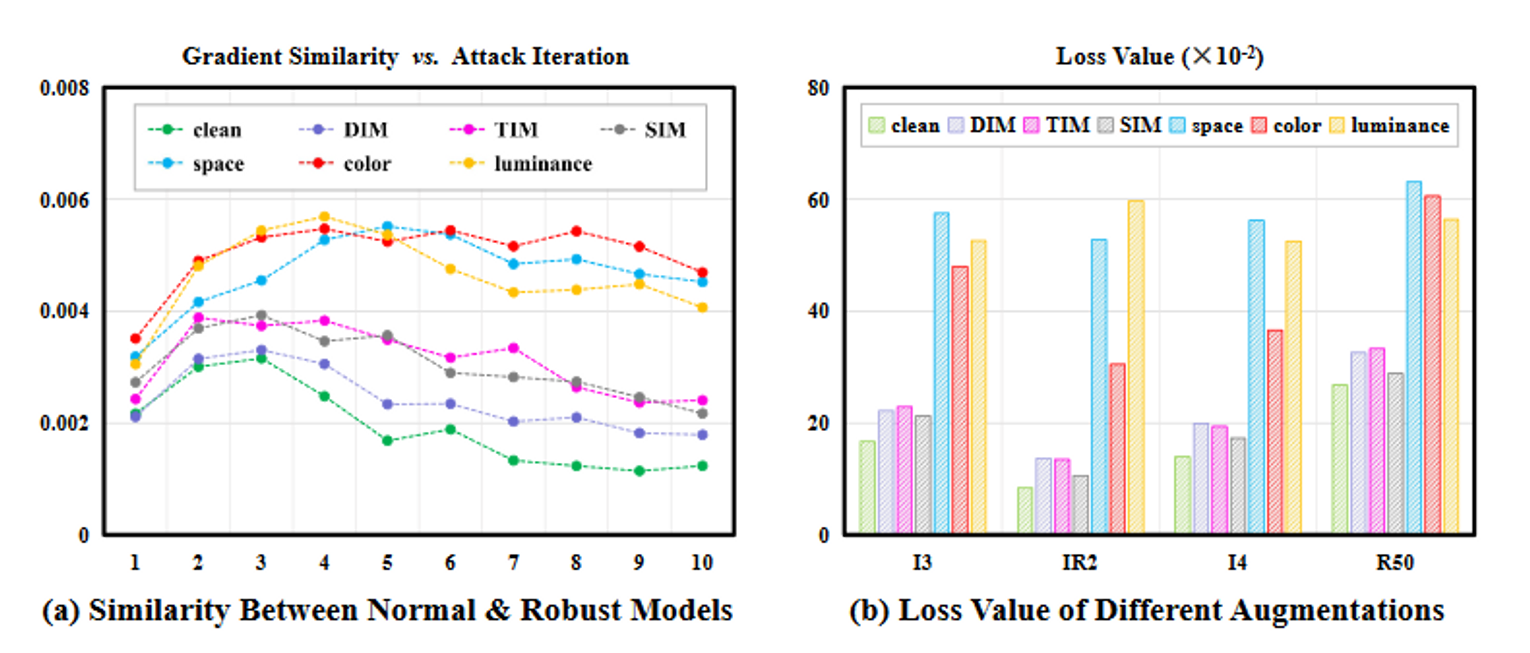
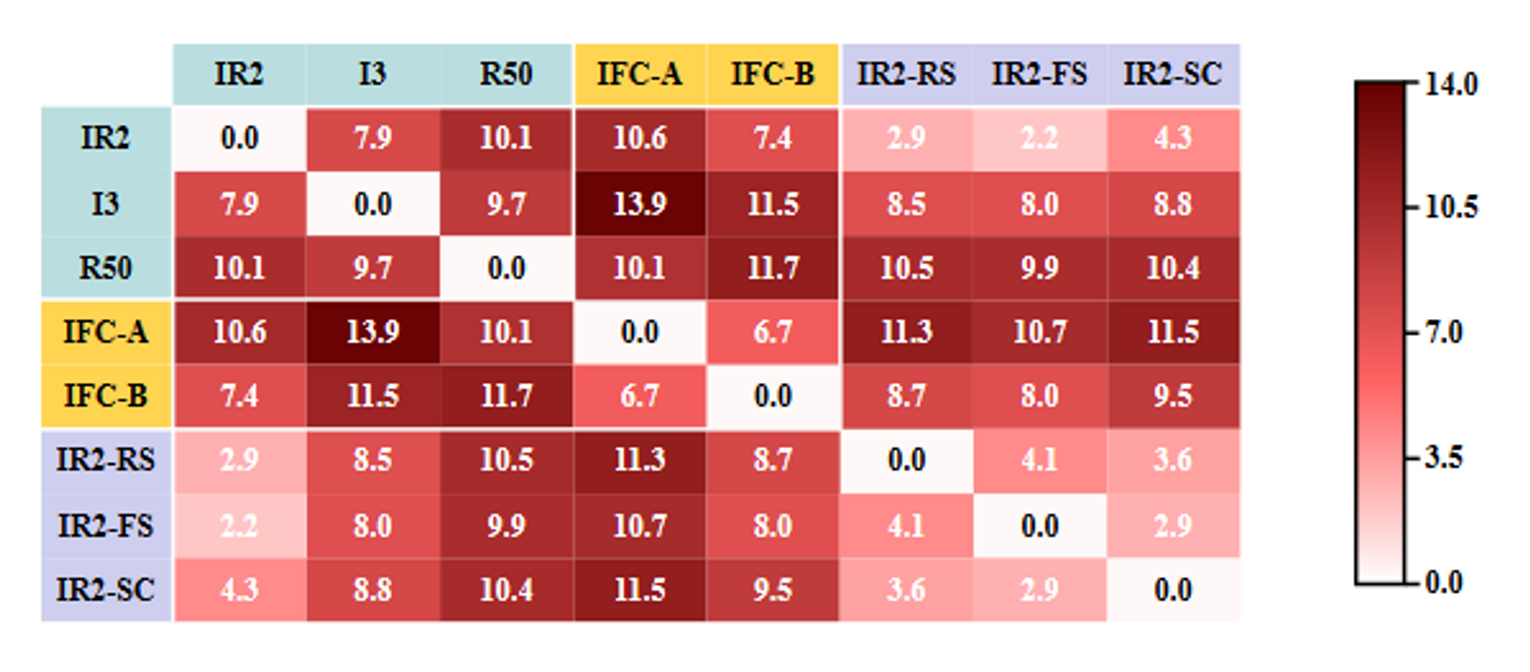
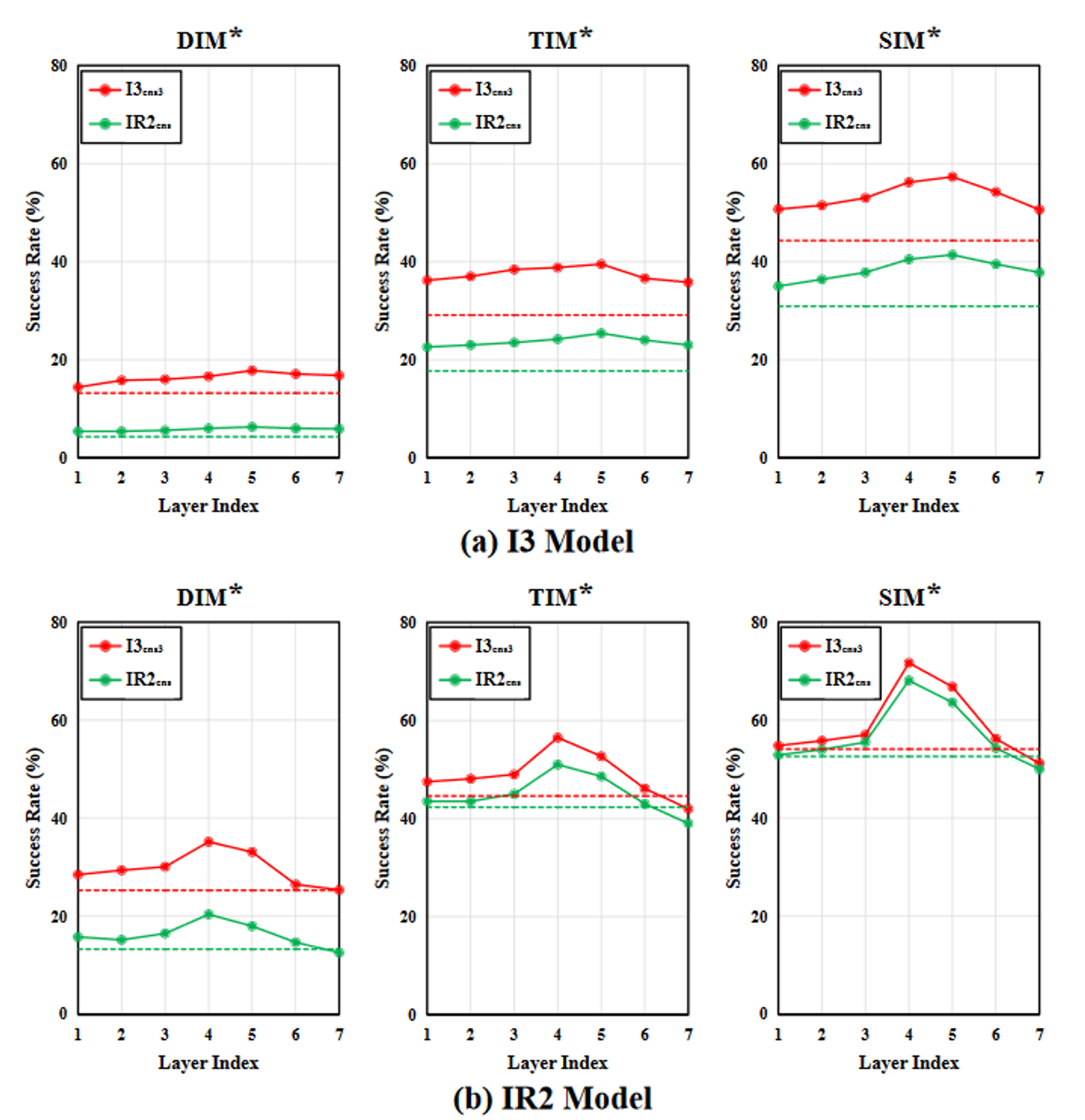
图(6)的含义：

• 原始模型IR2与其损坏版本之间的差异较大，甚至可以与其它vanilla模型(I3,R50)媲美
• 中间特征分类器和嵌入随机层的网络之间也表现出显著的差异性
• 级联组层在大多数情况下比随机缩放和特征平滑能给模型带来更大的多样性，可能会影响可迁移性的性能

单一模型攻击实验

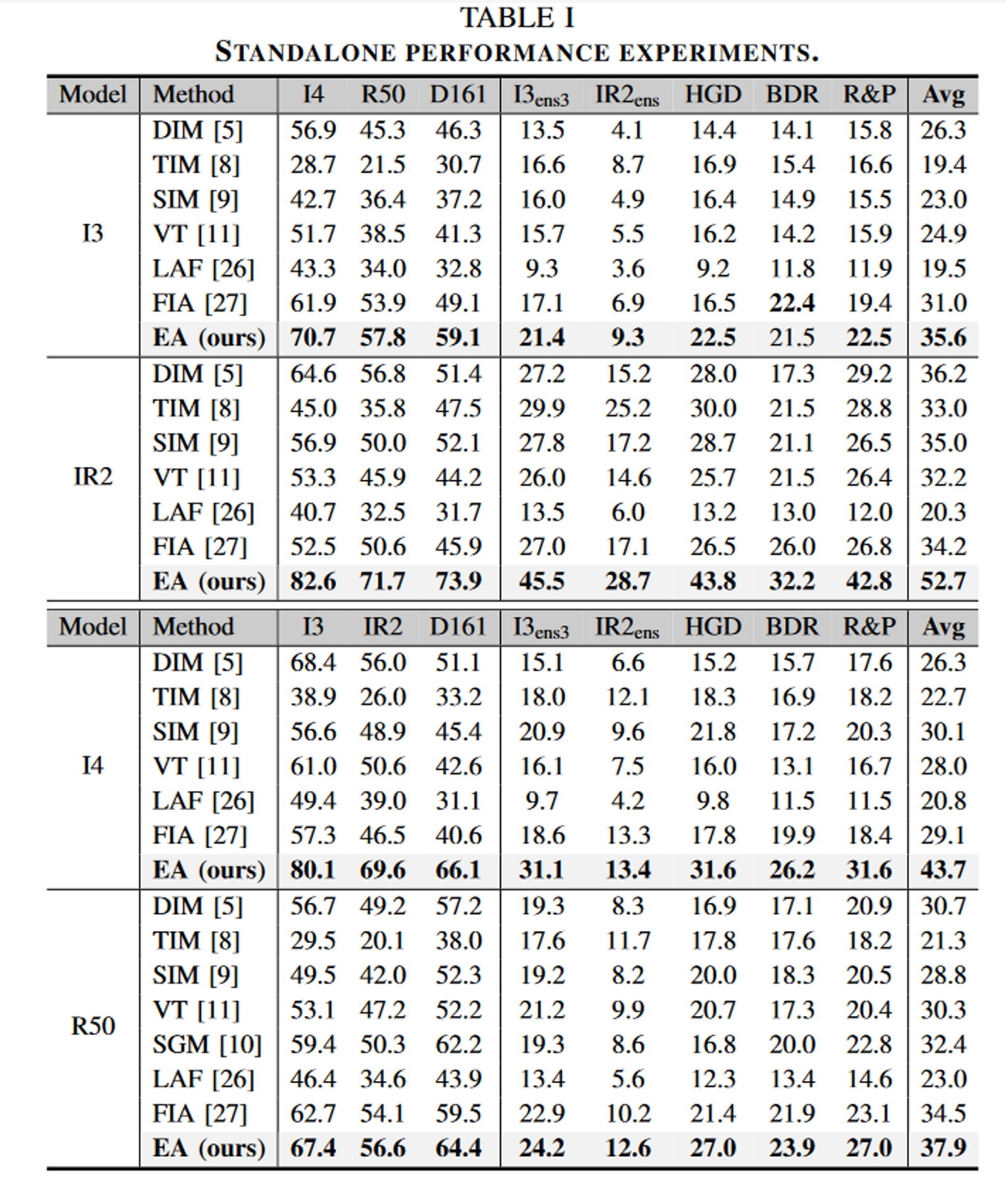
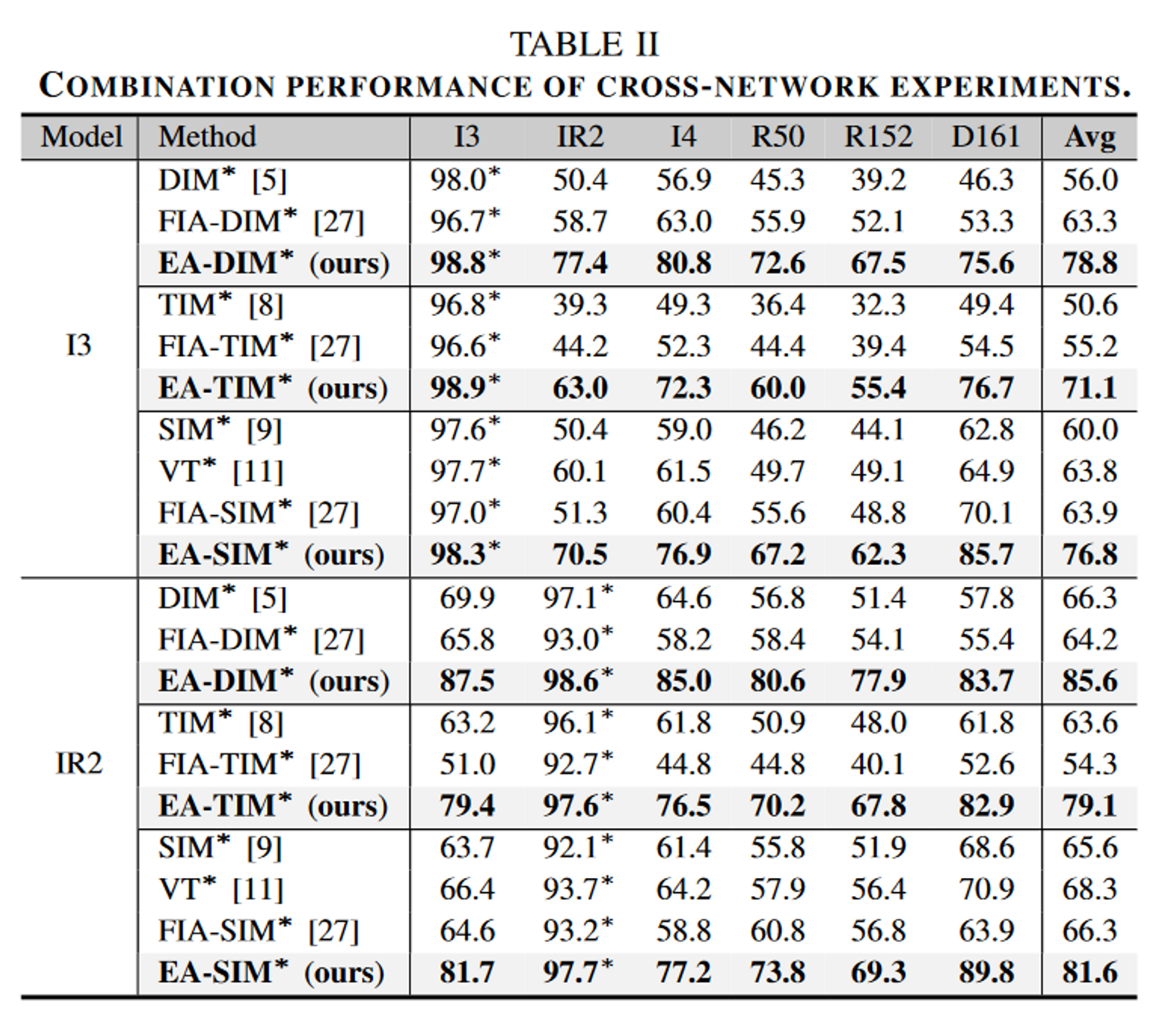
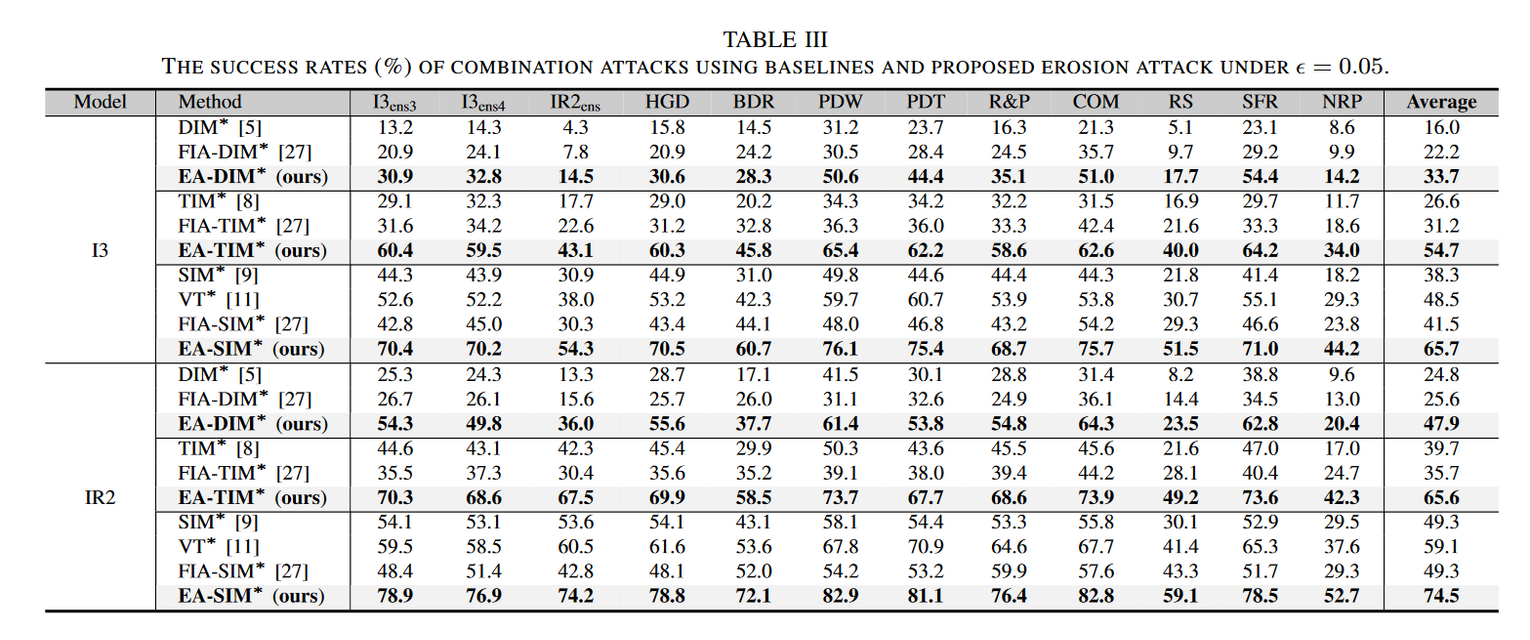
集成模型攻击实验

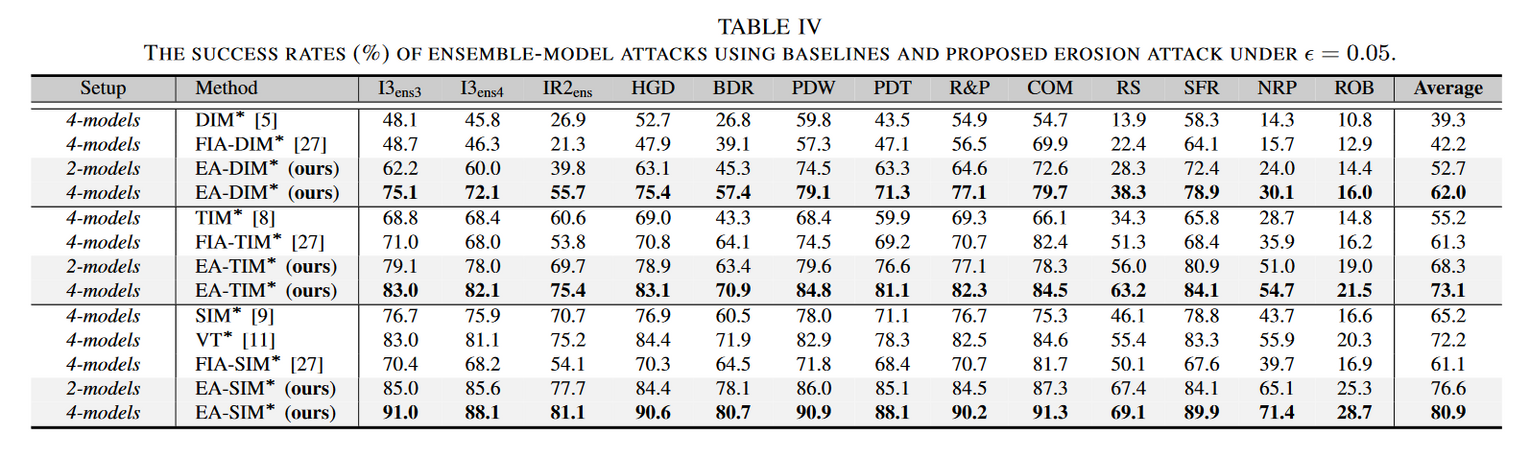
证实了该方法可以利用少量现有网络，以较低的微调成本来提高模型多样性，而不是简单巡礼那不同架构的新模型，并将其应用于标准的集成攻击来达到这一目的。

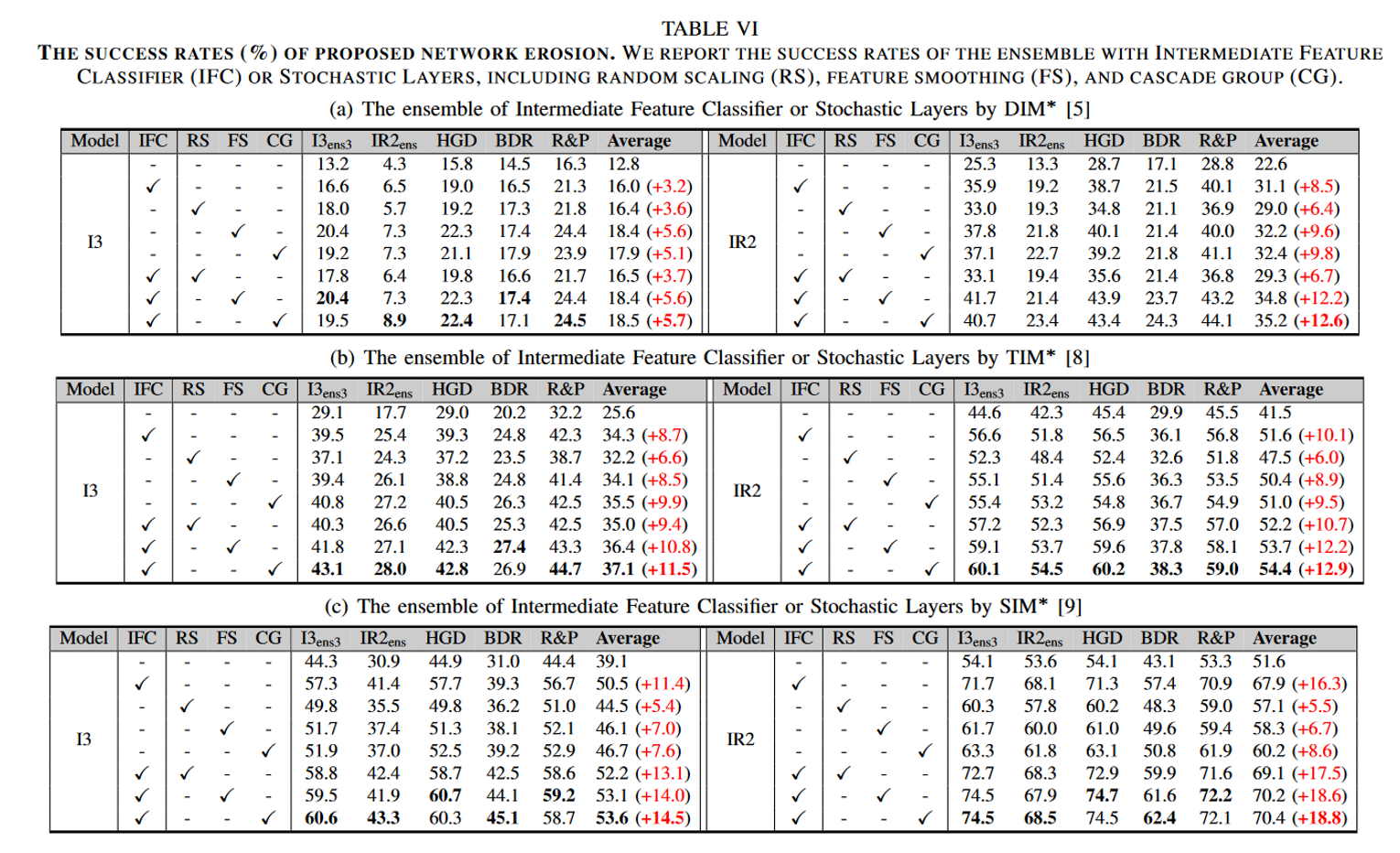
消融实验