Information

论文位置：[2308.02897] An Adaptive Model Ensemble Adversarial Attack for Boosting Adversarial Transferability (arxiv.org)

日期：2023-08

关键词：Adversarial Attack

出处：ICCV 2023

概述

以往的关于可迁移对抗攻击的工作大多研究梯度变化或图像变换来放大输入关键部位的失真，这些方法可以在有限差异的模型之间进行迁移，即从CNNs迁移到CNNs，但总是无法在差异较大的模型之间进行迁移，如从CNNs迁移到ViTs。或者，提出模型集成对抗攻击，将来自不同架构代理模型的输出进行融合，得到一个集成损失，使得生成的对抗样本更有可能迁移到其他模型，因其可以同时欺骗多个模型。

然而现有的集成攻击只是简单地将代理模型的输出进行均匀融合，无法有效捕获和放大对抗样本的内在迁移信息。本论文提出一种称为AdaEA的自适应集成攻击，通过监控每个模型的输出对对抗目标贡献的差异比例来自适应控制每个模型的输出的融合。此外，为了进一步同步更新方向，还引入了额外的视差减小滤波器。

背景

类似于传统的集成方法利用多个具有不同预测的弱学习器的智慧来提高整体精度，一系列研究提出利用代理模型的集成来生成能够成功攻击所有代理模型的对抗样本。从直觉上讲，该方法可以提高对抗样本的可迁移性，因其可以捕获内在的可迁移对抗信息，可以同时欺骗多个具有广泛差异的模型。

现有的大多数集成方法只是将所有模型的输出即（logits或loss）等量融合得到一个集成损失，用于实施基于梯度的攻击，这可能会限制模型集成攻击的潜在能力。

由于忽略了每个模型的个体特征，这样的集成是欠优化的。

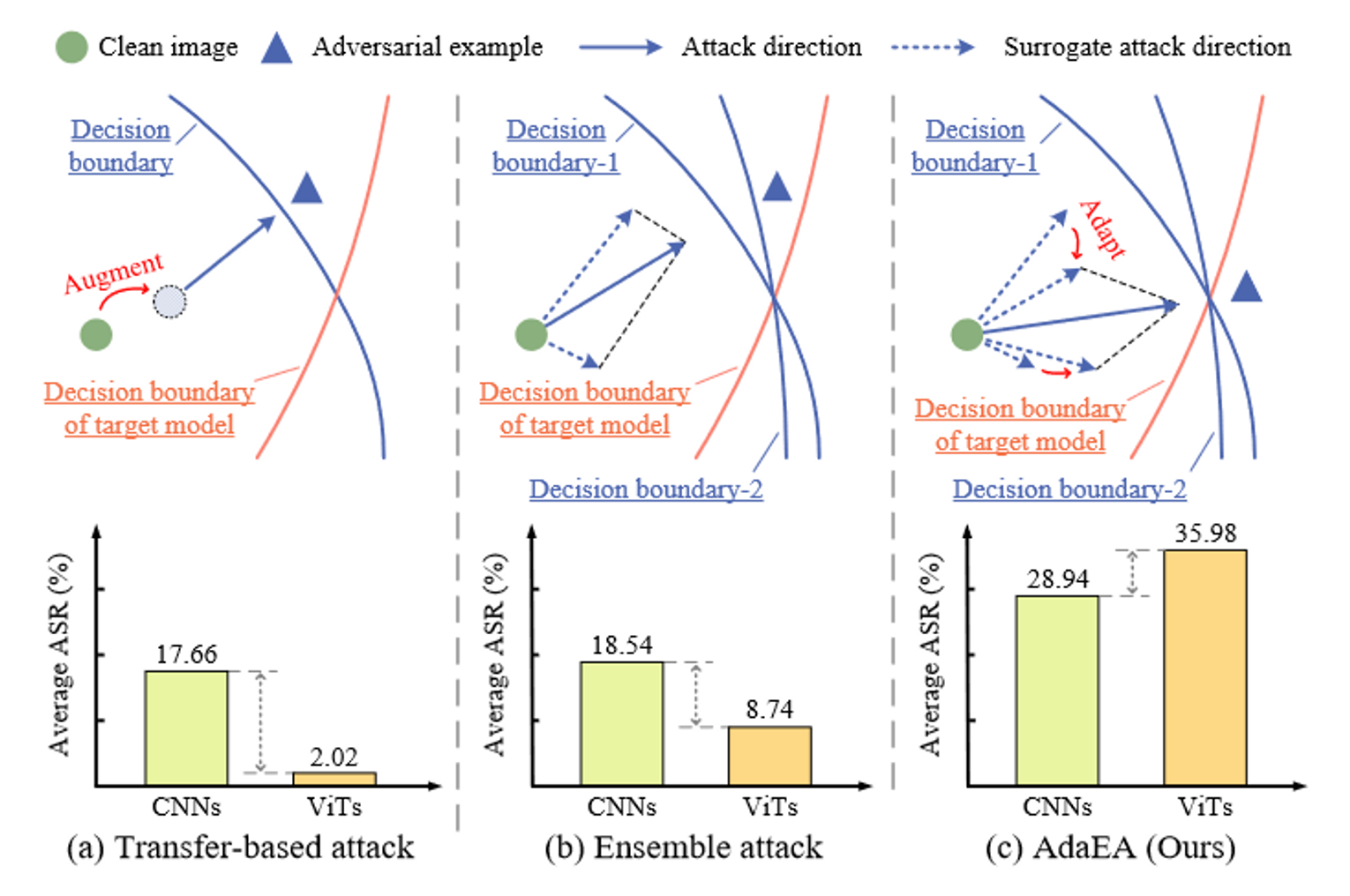
图1，不同攻击方案及性能概述。(a)基于迁移的方法通过强化图像中的关键部分来提高攻击的可迁移性，但由于对抗信息有限，无法在差异较大的DNN之间进行转移。(b)模型集成攻击通过集成多个代理模型来寻找更具可迁移性的攻击，但现有工作普遍忽略了每个模型的个体特征，导致结果不够理想。(c)本论文的AdaEA通过放大每个代理模型中的可迁移信息来进行自适应集成，并取得了显著改进。

本论文重点研究模型集成对抗攻击，以提高对抗样本的可迁移性。可以观察到，简单地对集成模型的输出进行平均忽略了每个模型的优势，在融合过程中，从一个模型捕获的可迁移信息可以被另一个模型平滑，从而导致结果欠优化。

为了解决这个问题，本论文提出通过自适应梯度调制(Adaptive Gradient Modulation, AGM)策略对每个模型的输出进行自适应集成。具体而言，本论文定义了对抗比来评估代理模型之间对整体对抗目标的贡献差异，然后利用对抗比自适应地调节梯度融合，为生成地对抗样本中可迁移信息地放大提供更多的努力。

而且，集成梯度可能与代理模型的个体梯度存在较大差异甚至对立，这已经被证明与集成中的过拟合问题存在相关性。因此，我们进一步引入了一个视差降低滤波器(DRF)，通过计算视差图来降低代理模型之间的差异并同步更新方向。

最后，通过应用上述两种机制，可以增强对抗攻击的可迁移性。称之为AdaEA。

本论文的贡献：

提出一种自适应集成对抗攻击，成为AdaEA，为具有广泛结构差异的模型提供了更全面的集成攻击，如CNNs和ViTs。
AdaEA从梯度优化的角度看待集成攻击，通过AGM策略控制优化过程，并通过DRF减小视差以同步优化方向。
与现有的集成方法相比，所提出的AdaEA不仅可以显著提高集成效果，而且与现有的基于迁移的梯度攻击相结合，可以持续地提高攻击性能。

方法

简述

提高对抗样本地可迁移性旨在使从白盒代理模型生成地对抗样本保持对抗，从而抵制黑盒模型。通常，使用基于梯度地方法迭代寻找白盒模型的对抗扰动可以由下式给出：

$x_{t+1}^{adv}=x_t^{adv}+\alpha sign(\nabla_{x_t^{adv}}\mathcal{L}(f(x_t^{adv}),y))$，(1)

其中：

$sign(\cdot)$是符号函数
$\alpha$是步长
$\nabla_{x_t^{adv}}\mathcal{L}$是损失函数关于$x_t^{adv}$的梯度

直观上，在白盒环境下由于$\nabla_{x_t^{adv}}\mathcal{L}$是已知的，可以达到很高的攻击成功率，然而黑盒环境由于梯度位置，不同模型的梯度不同，攻击成功率会下降。

为了使生成的对抗样本对广泛类别的模型具有对抗性，集成攻击时增强攻击可迁移性的有效策略，其基本思想是利用多个白盒模型的输出得到平均模型损失，然后应用基于梯度的攻击生成对抗样本，将式(1)变化可得：

$x_{t+1}^{adv}=x_t^{adv}+\alpha sign(\nabla_{x_t^{adv}}\mathcal{L}(\sum\limits_{k=1}^Kw_kf_k(x_t^{adv}),y))$，(2)

其中：$w_k$为第$k$个代理模型$f_k$的集合权重，$∀w_k≥0$且$\sum\limits_{k=1}^Kw_k=1$，$K$为代理模型个数

现有的集成方法一般通过平均提带模型的logits、预测概率或loss来获得用于生成梯度信息的集成loss。然而，这种简单的集成忽略了代理模型之间的个体方差，从而显著限制了整体的攻击性能。

自适应集成对抗攻击AdaEA

重点研究遵循公式(2)的集合方法。与以往工作直接对代理模型的输出进行平均不同，本论文提出了配备AGM和DRF机制的AdaEA来修正梯度优化过程，以提高生成对抗样本中的可传递信息。具体来说，AGM首先通过定义的对抗比来调节每个集成模型的梯度，该对抗比识别每个代理模型对整体对抗对象的贡献差异，然后DRF通过过滤掉集成梯度中的视差部分来进一步同步梯度更新方向。AdaEA概述如图：

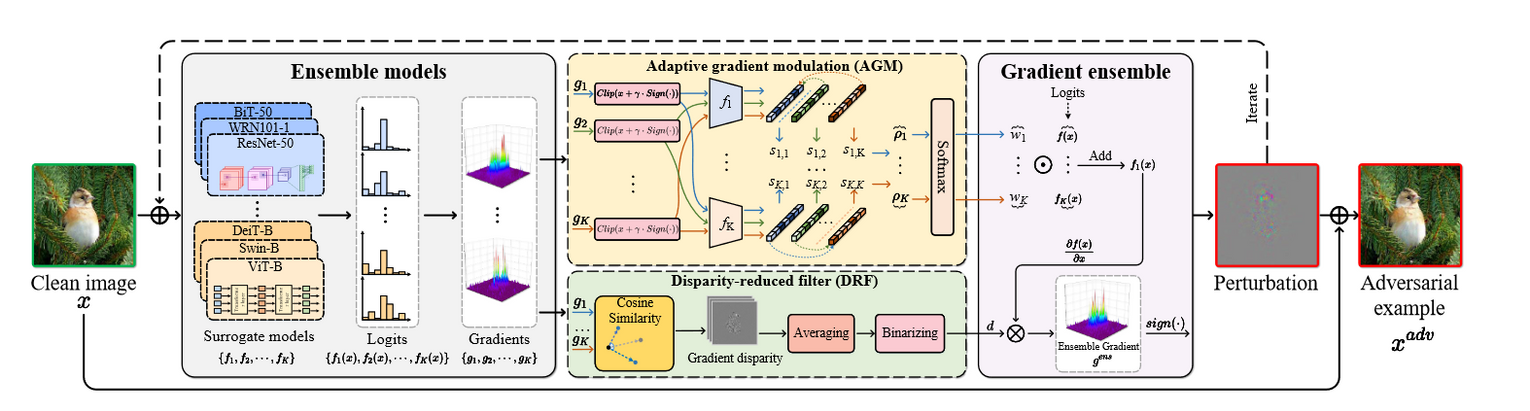
图3，AdaEA概述，将CNNs和ViTs得到的梯度输入到AGM和DRF中得到集成梯度，用于生成基于梯度攻击的对抗样本

自适应梯度调制

在通过输入图像得到每个代理模型$f_i(x)$和梯度信息$g_i=\nabla_{x_t^{adv}}\mathcal{L}(f_i(x_t^{adv}),y)$后，通过提出检测其对对抗攻击目标贡献的差异来自适应地调节模型集成。

具体来说，对于第$i$个集成模型$f_i$，通过测试由$g_i$生成的对抗样本对其他模型的攻击性能来评估$g_i$中潜在的对抗可迁移性，将其定义为对抗比，然后根据每个模型的对抗比来调整集成权重。这里首先通过计算来进行测试过程：

$s_{k,i}=-\mathbf{1}_y\cdot \log (\text{softmax}(\mathbf{p}_k[x_t^{adv}+\alpha sign(g_i)]))$，(3)

其中：

$\mathbf{p}_k(\cdot)$表示从$f_k$输出的logits值，$\mathbf 1_y$是真实logits值
$s_{k,i}$是在使用来自第$i$个模型的梯度生成的对抗样本上的第$k$个模型los

定义对抗比$ρ_i$：

$ρ_i=\frac{\beta}{K-1}\sum\limits_{k=1,k≠i}^K\frac{s_{k,i}}{s_{k,k}}$，(4)

其中$\beta$为控制集合加权效果的超参数。

值得注意的是$ρ_i$的值越大，表示从$g_i$生成的对抗样本的迁移攻击越好，意味着$g_i$包含了更多可迁移的对抗信息。通过此可以弄清楚哪些模型可以提供更多的通用对抗信息，并自适应地分配更高地集成权重。

因此，根据每个模型的对抗比，我们使用softmax函数对每个模型的集成权重进行归一化：

$w_1^*,w_2^*,...,w_K^*=\text{softmax}(ρ_1,ρ_2,...,ρ_K)$，(5)

利用得到的$w_i^*$，每个具有更多潜在对抗可迁移性信息的代理模型的输出在方程(2)的集成梯度中被放大，从而导致在黑盒模型上有更高的转移攻击成功率。

视差降低滤波器DRF

代理模型的梯度优化方向在很大范围内变化，有时梯度会朝着相反的方向前进，结果导致对集成模型的过度拟合。为了解决这个问题并同步更新方向，额外引入减少视差的滤波器来减少代理模型之间的梯度方差。

首先用余弦相速度来评估代理模型中梯度的偏差，并通过将相似度得分与其他模型的梯度求平均来计算视差图$d_i$：

$d_i^{(p,q)}=\frac1{K-1}\sum\limits_{k=1,k≠1}^K\cos(\vec{g}_i^{(p,q)},\vec{g}_k^{(p,q)})$，(6)

其中：

$\cos(\cdot)$表示余弦相似度函数
$\vec{g}_i^{(p,q)}、\vec{g}_k^{(p,q)}$分别表示通过梯度$g_i$和$g_k$通道从位置$(p,q)$提取的向量

通过对所有的$d_i$求平均得到最终的集成梯度视差图$d$。

然后，我们通过使用一个滤波器$\mathbf{B}$来清理集合梯度中的视差部分：

$\mathbf B(p,q)=\begin{cases}0,&\text{if}\ d_i^{(p,q)}≤η\\ 1,&\text{otherwise}\end{cases}$，(7)

其中$η$为视差滤波的容差阈值。

通过滤除集合梯度中的视差部分，可以实现梯度优化方向的同步。为此，可以通过改写公式(2)得到集合梯度：

$g_{t+1}=\nabla_{x_t^{adv}}\mathcal{L}(\sum\limits_{k=1}^Kw_k^*f_k(x_t^{adv}),y)\otimes\mathbf{B}$，(8)

其中$\otimes$表示按元素相乘。

因此，代理模型之间的差异可以被抑制。

AdaEA整体流程如算法1所示：

实验

参数设置

对于baselines和AdaEA：

使用$l_∞-norm$下迭代$20$次的I-FGSM作为基本攻击方法，并在对抗样本生成过程中设置：
- 最大扰动$\epsilon=8/255$
- 步长$\alpha=2/255$
超参数:
- 在DRF中取视差滤波容差阈值$η=-0.3$
- 在AGM中取控制集成加权效果超参数$\beta=10$

主要结果

一般攻击性能

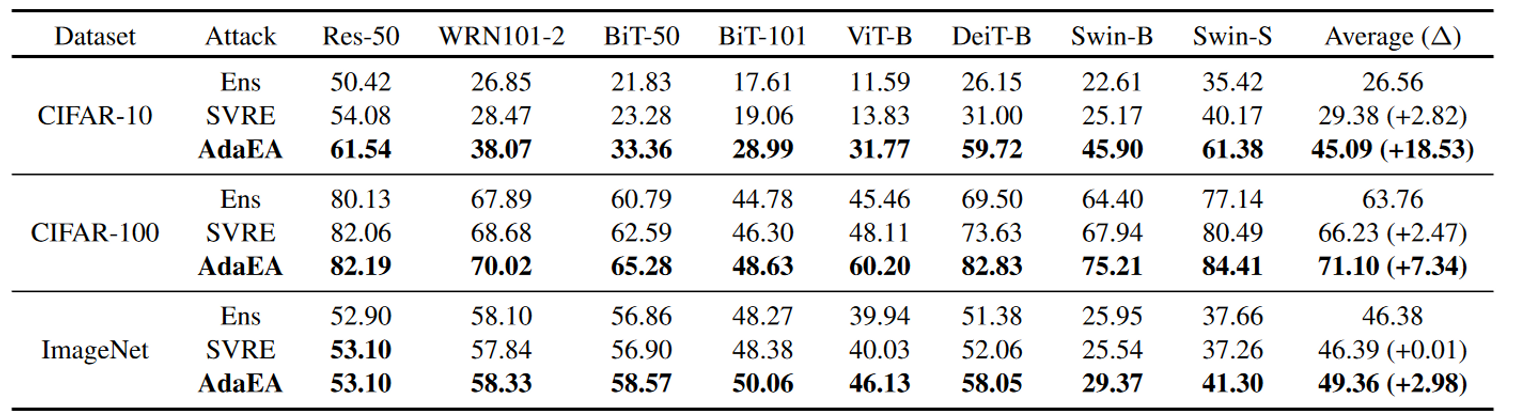
$表1，针对8个自然训练模型的黑盒攻击成功率。加粗表示最好结果，\triangle表示相对于baseline的改进$

与基于迁移的攻击的结合

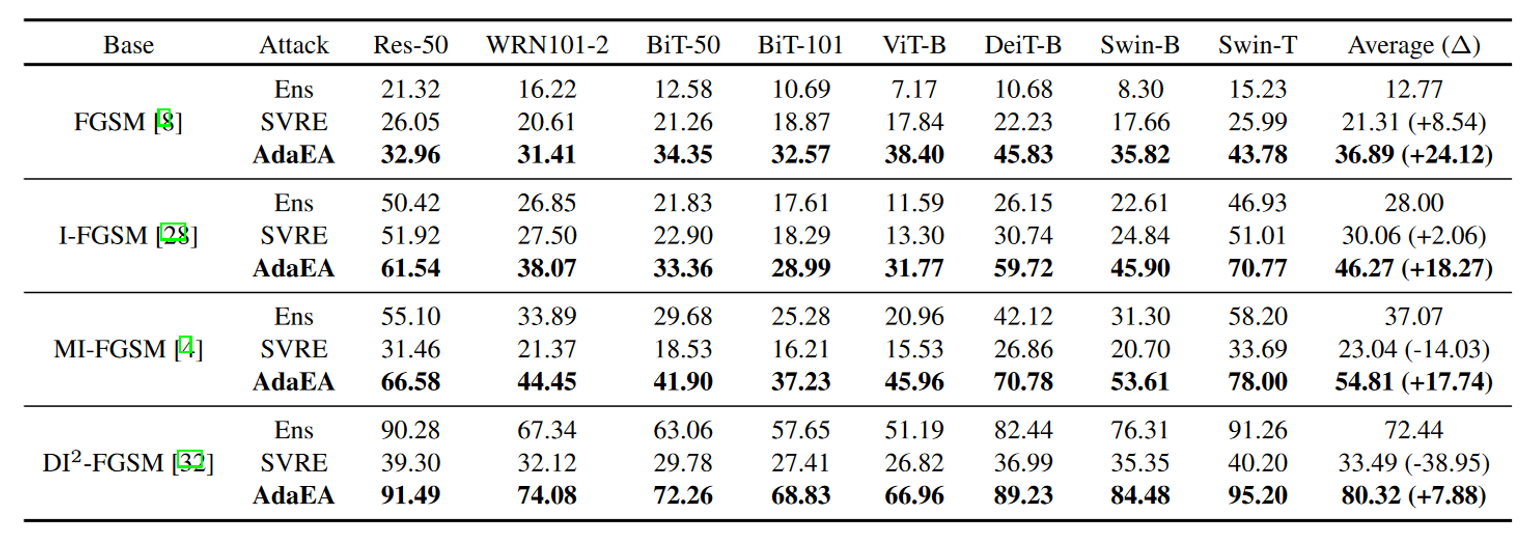
表2，基于不同攻击方法的集成攻击在CIFAR10上生成对抗样本的攻击成功率。

对先进防御的攻击

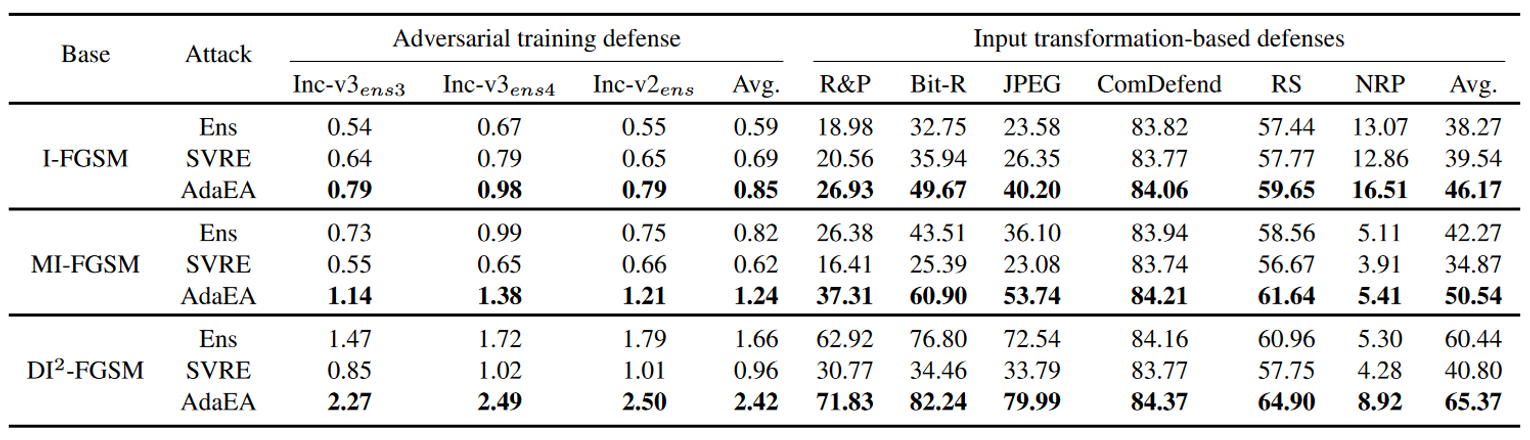
表3，在CIFAR-10上对抗3中对抗训练模型和6种高级防御方法的鲁棒性准确率。基于输入转换的防御结果是所有目标模型的平均结果。

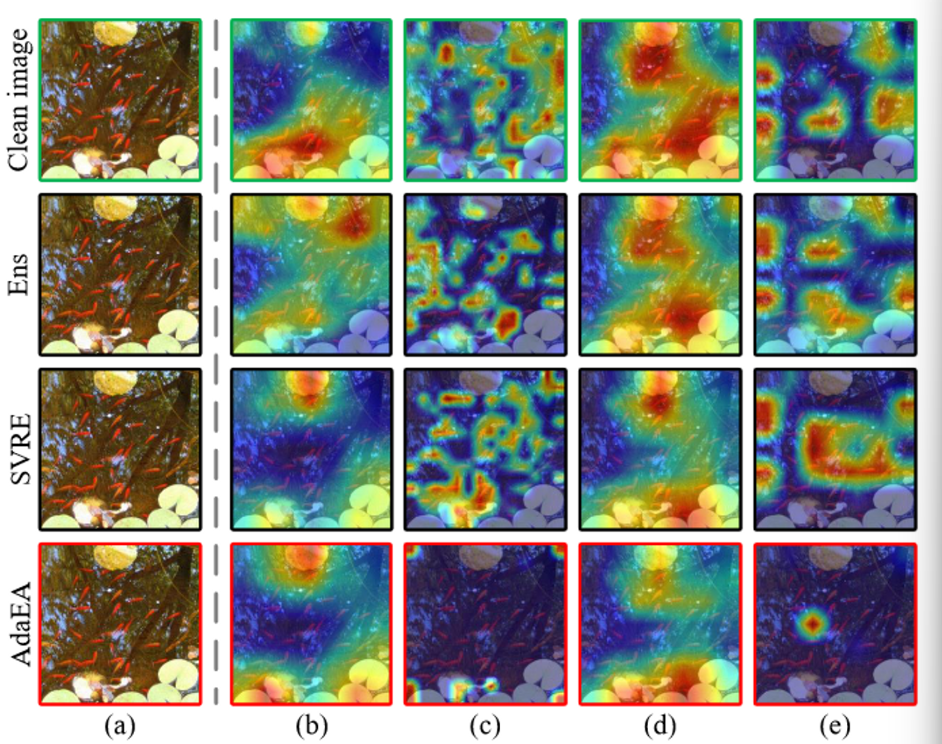
图4，代理模型和黑盒模型中不同输入的热力图。(a)为输入图像，包括干净图像和每种攻击方法生成的对抗样本。(b)-(e)分别为代理模型(Res-18、ViT-T)和黑盒模型(WRN50-2、Swin-T)

从图4(b)和(c)中可以观察到，与干净图像相比，白盒模型在所有生成的对抗样本上的注意力都发生了变化，这表明生成的对抗样本可以有效触发这些模型的错误预测。然而，当转移到黑盒模型时，Ens和SVRE方法无法误导热土与干净图像相似的模型注意力，如图4(d)-(e)中第2-3行所示。相比之下，得益于AdaEA中AGM-DRF方案对潜在内在对抗信息的放大，生成的对抗样本仍然能够欺骗图4(d)-(e)中注意力剧烈变化的黑河模型的注意力。

消融实验

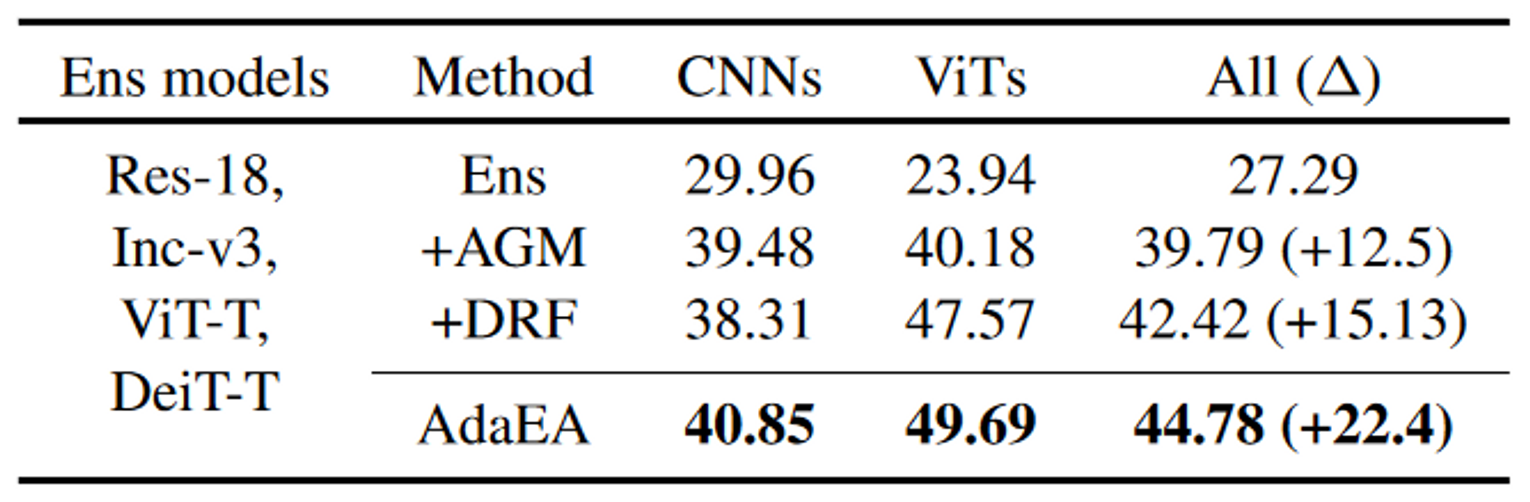
关于AdaEA组成部分。检验AdaEA中AGM和DRF机制的有效性。具体来说执行了四种集成方法：
- 朴素集成攻击
- 集成AGM
- 集成DRF
- AdaEA在黑盒攻击中同时涉及AGM和DRF
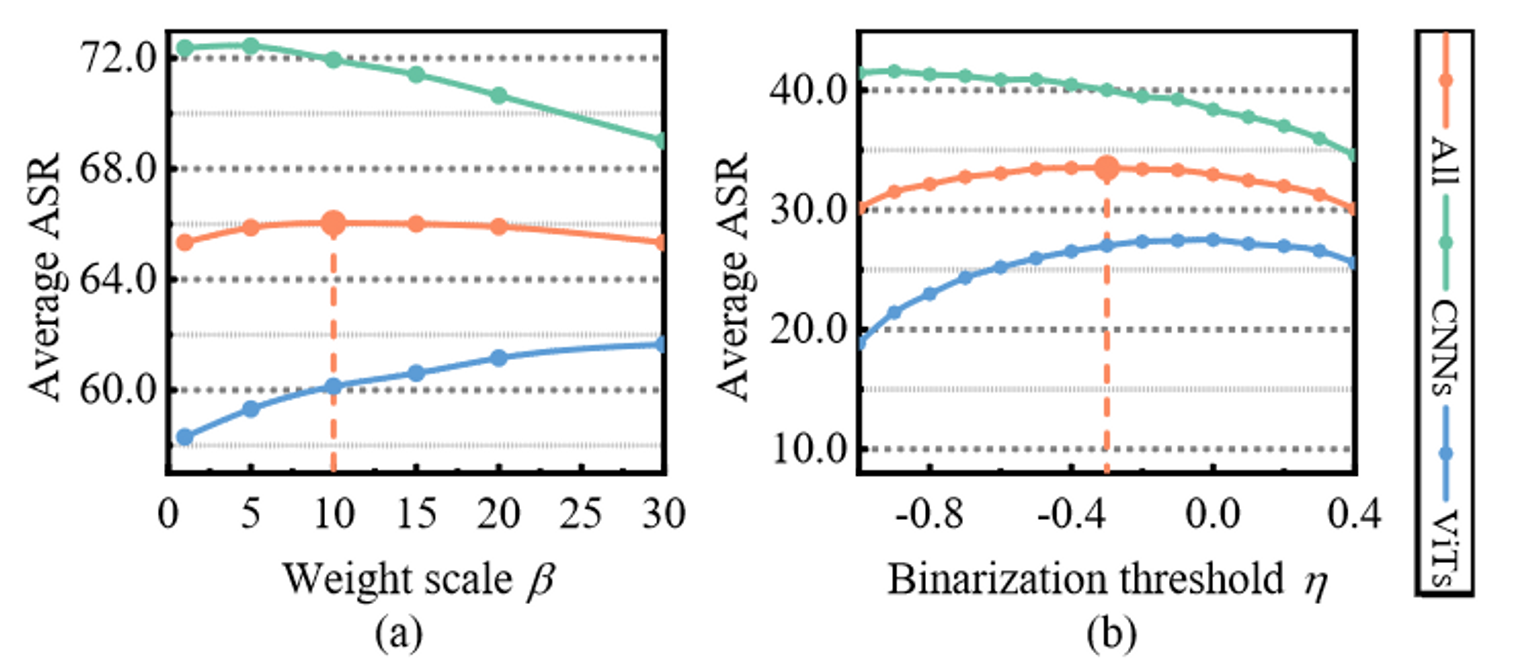
关于超参数敏感性。研究AdaEA对方程(4)中权重尺度$\beta$和公式(7)中的二值化阈值$η$的敏感性。

$图5，AGM中加权尺度\beta和(b)DRF中二值化阈值η的消融研究$

进一步分析

代理模型的数量对可迁移性有何影响？

从表5可以看出，随着代理模型的数量增加，整体攻击成功率从第1行到最底层逐行提高。直观上，由于可以捕获更多的对抗信息，使用更多的代理模型可以导致更好的可迁移性。更重要的是，AdaEA在不考虑集成模型数量的情况下，始终如一地提高了集成攻击性能。
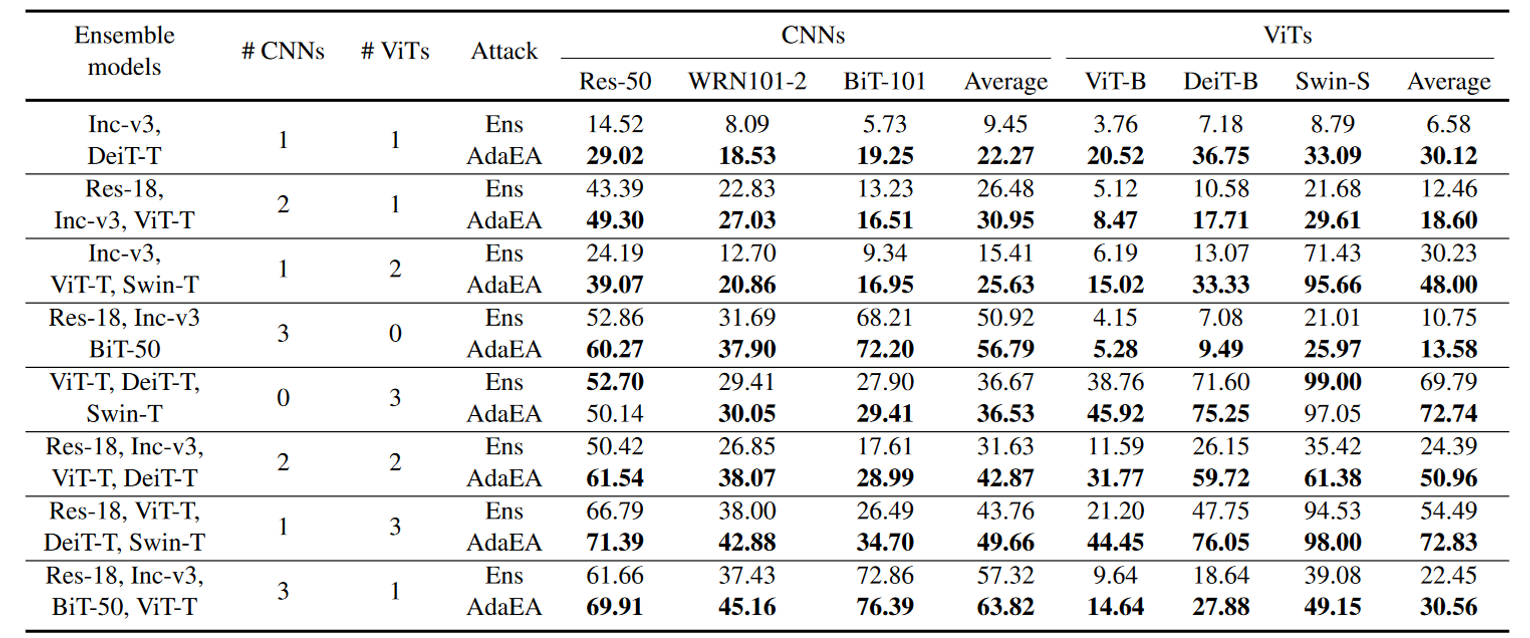
代理模型中不同的CNNs与ViTs的比例如何影响整体的可迁移性？

由表5第二行、第三行、第九行，随着代理模型中CNN数量的增加，对CNN的攻击率明显提高，相比之下对ViTs的攻击成功率不高。这表明当CNNs在代理模型中站主导地位时，集成梯度更侧重于CNNs的梯度。

当CNNs与ViTs比例变为0：3时，集成攻击仍然表现出对CNNs的高转移率。这一现象表明，从与CNNs转移到ViTs相比，从ViTs转移到CNNs更容易发生攻击，我们将其归因于VITs更复杂的框架和全局建模能力，使得ViTs能够提取更多通用的对抗信息。