[文献阅读]基于特征重要性感知攻击的可迁移对抗攻击-FIA

Information

论文位置：[2107.14185] Feature Importance-aware Transferable Adversarial Attacks (arxiv.org)

日期：2021-07

关键词：Adversarial Attack

出处：ICCV 2021

代码仓库：https://github.com/hcguoO0/FIA

背景

• 深度神经网络（DNNs）容易受到对抗样本对深度神经网络的影响在研究神经网络的内部缺陷和提高其鲁棒性方面发挥着重要作用。
• 传统攻击方法如FGSM、BIM等制作的对抗样本往往由于对源模型的过拟合而表现出较弱的可迁移性。
• 现有的可迁移性的对抗性扰动直接在中间层进行攻击，没有干扰输出层，且最大化内部特征失真，以增强可迁移性；然而其通过不加区分地扭曲特征来生成对抗样本，而没有意识到图像中物体地内部特征，因此容易陷入特定于模型的局部最优。
• 本论文提出了一个特征重要性感知攻击的方法，通过破坏主导不同模型决策的关键对象感知特性（也就是破坏主导模型决策的一些特性），从而显著提高对抗样本的迁移性。针对特定于模型的特征，我们引入了聚合梯度，它将有效地一直特定于模型的特征，同时提供特征的对象感知重要性。

• 本论文的主要贡献：
  • 提出特征重要性感知攻击（Feature Importance-aware Attack，FIA），通过破坏主导不同模型决策的关键对象感知特征来增强对抗样本的可迁移性；
  • 分析了现有工作相对较低的可性背后的基本原理，即对特定于模型的“噪声”特征的过度拟合，针对这些特征引入聚合梯度，以指导生成更多可迁移的对抗样本。

特征重要性感知攻击（FIA）

预备

对于一个分类模型$f\theta:x\mapsto y$，其中x和y分别表示干净图像（原始图像/自然图像）和真实标签，θ表示模型的参数。我们的目标是生成一个对抗样本$x^{adv}=x+\epsilon$，以通过设计出扰动$\epsilon$来误导分类器，也即使得$f\theta(x^{adv})≠y$。通常，$\ell_p-$范数用于正则化扰动。因此，对抗样本的生成可以表述为如下式的优化问题：

• $\large arg \mathop{max}\limits_{x^{adv}}J(x^{adv},y),s.t. ||x-x^{adv}||_p≤\epsilon$， (1)
  • 其中$J(·,·)$为损失函数，测量真实标签与预测标签间的差距（即交叉熵）
  • $argmax\ g(t)$表达的是定义域的一个子集，且盖子集中任一元素都可使函数$g(t)$取最大值
  • 在这项工作中$p=∞$

特征重要性感知攻击概述

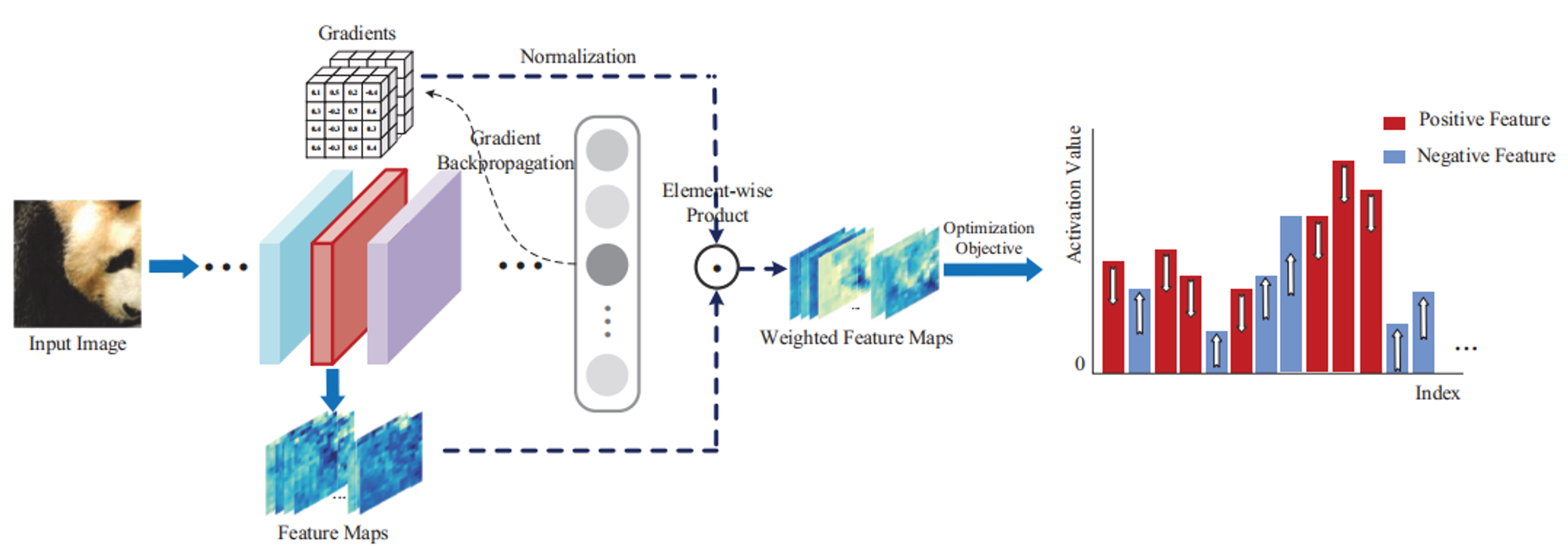
特征重要性

不同的网络会提取排他性特征来更好地适应数据域，这就产生了特定于模型的特征表示，因而对抗样本的生成需要由来自源模型的与模型无关的关键特征来指导，这被称为特征重要性。

基于梯度聚合的特征重要性

由于特征重要性与特征对最终决策的贡献程度成正比，一个方法是通过下式计算关于$f_k(x)$的梯度来求得特征重要性：

• $\Large \Delta^x_k=\frac{\partial l(x,t)}{\partial f_k(x)}$， (2)
  • 令$f$表示源模型，则$f_k(x)$表示来自第$k$层的特征图
  • $l(·,·)$表示相对于真实标签$t$的对数输出

可以看出原始梯度图和原始特征图在视觉上都是有噪声的，也就是在非目标区域上存在脉冲较大的梯度，这可能时由于模型特有的解空间造成的；但经过聚合之后的特征图和梯度图就消除了这样的影响，只在目标区域存在脉冲较大的梯度。可以说，与原始梯度相比，聚合梯度更加干净、更加关注对象，在可转移的视角中提供了更好的特征重要性。

聚合梯度

为了抑制特定于模型的信息，本论文提出聚合梯度（aggregate gradient），聚合了来自随机变换$x$的梯度，如下图所示。

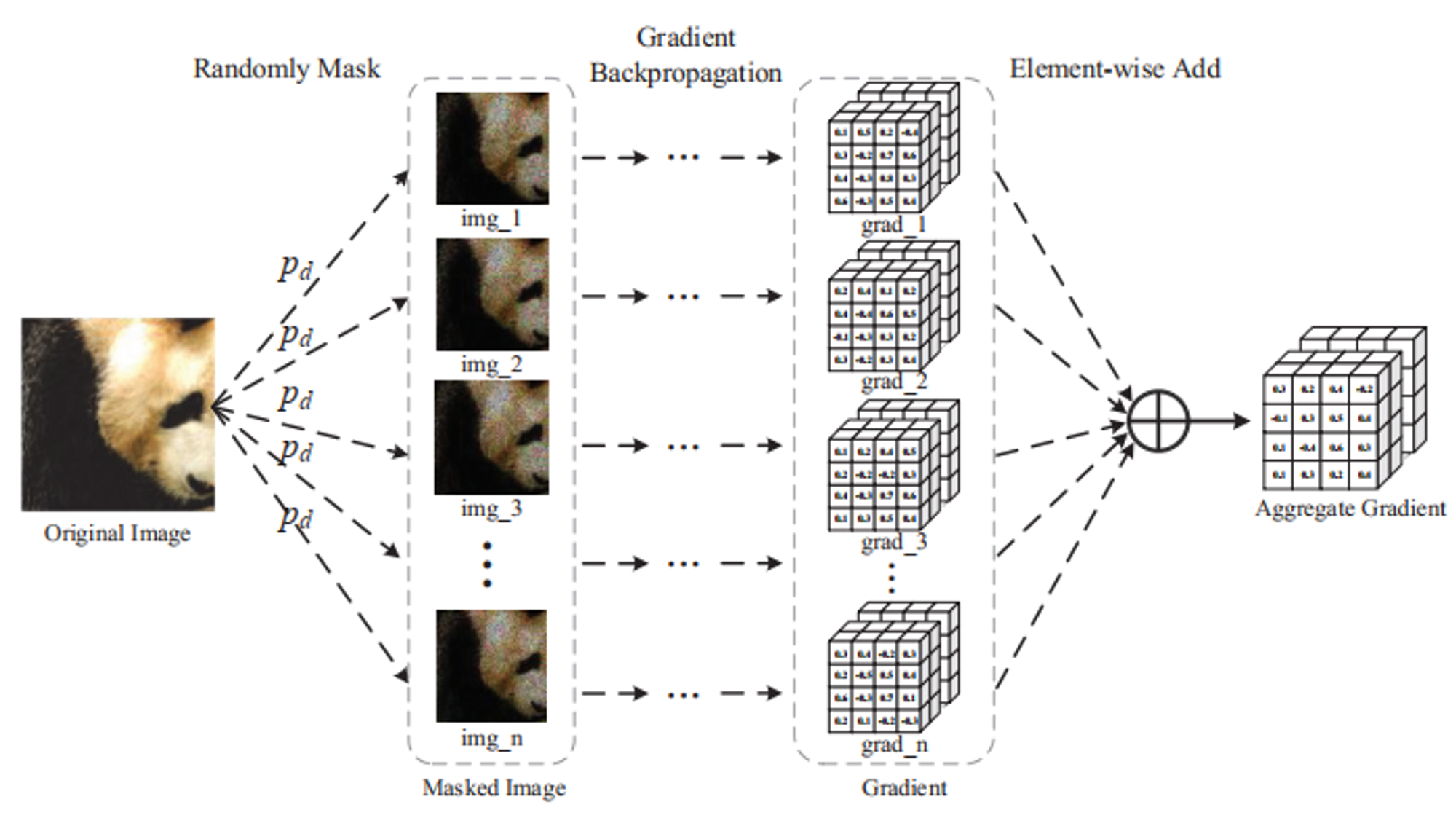
梯度聚合公式：

• $\large\bar{\Delta}k^x=\frac{1}{C}\sum\limits^N{n=1}\Delta^{x\odot M^n{p_d}}_k,M{p_d}\sim Bernoulli(1-p_d)$， (3)
  • $M_{p_d}$表示和原图x大小相同的二进制矩阵（符合服从参数为$1-p_d$的伯努利分布）
  • $\bigodot$表示点积
  • 标准化数$C$是$\ell_2-$范数，用以约束聚合梯度
  • $N$表示应用于输入$x$的随机掩码的数量
  • $p_d$为下降率

即首先将原图与随机掩码图像进行点积，然后将结果输入到模型中求第k层特征图的梯度，最后将这些梯度进行相加（聚合），并使用$\ell_2-$范数来做一个约束，得到聚合梯度。

$\ell_2-$范数：定义为向量所有元素的平方和的开平方

由于语义目标感知/重要特征/梯度对上述的这个变换是鲁棒的，但是一些特定模型的梯度或者特征容易受到转换的应向，因此那些鲁棒的可迁移的特征将会在聚合后被突出显示，而其他的梯度将会被中和。

攻击算法

根据上述的特征重要性（即聚合梯度$\bar\Delta_k^x$），本论文有如下损失函数公式来抑制特征重要性，以指导对抗样本$x^{adv}$的生成：

• $\large \mathcal{L}(x^{adv})=\sum(\Delta \odot f_k(x^{adv}))$， (4)

  为了简便而将$\bar\Delta^x_k$表示为$\Delta$

直观而言，修正特征以靠近真实标签的重要特征在特征重要性$\Delta$中占有较高的比重，且$\Delta$的符号给修正提供了方向。生成可迁移的对抗样本的目的是减少具符号为正的$\Delta$的重要特征，增加符号为负的$\Delta$对应的重要特征。因此可通过最小化式(4)来实现。

最后，将式(1)带入到式(1)，得到最终的对抗样本生成公式：

$\large arg\mathop{min}\limits{x^{adv}}\mathcal{L}(x^{adv}),\ s.t.\ ||x-x^{adv}||∞≤\epsilon$， (5)

采用MIM算法求解式(5)算法如下：

MIM算法是一种子监督表征学习方法。其主要思路是对输入图像进行分块和随机掩码操作，然后对掩码区域进行预测。

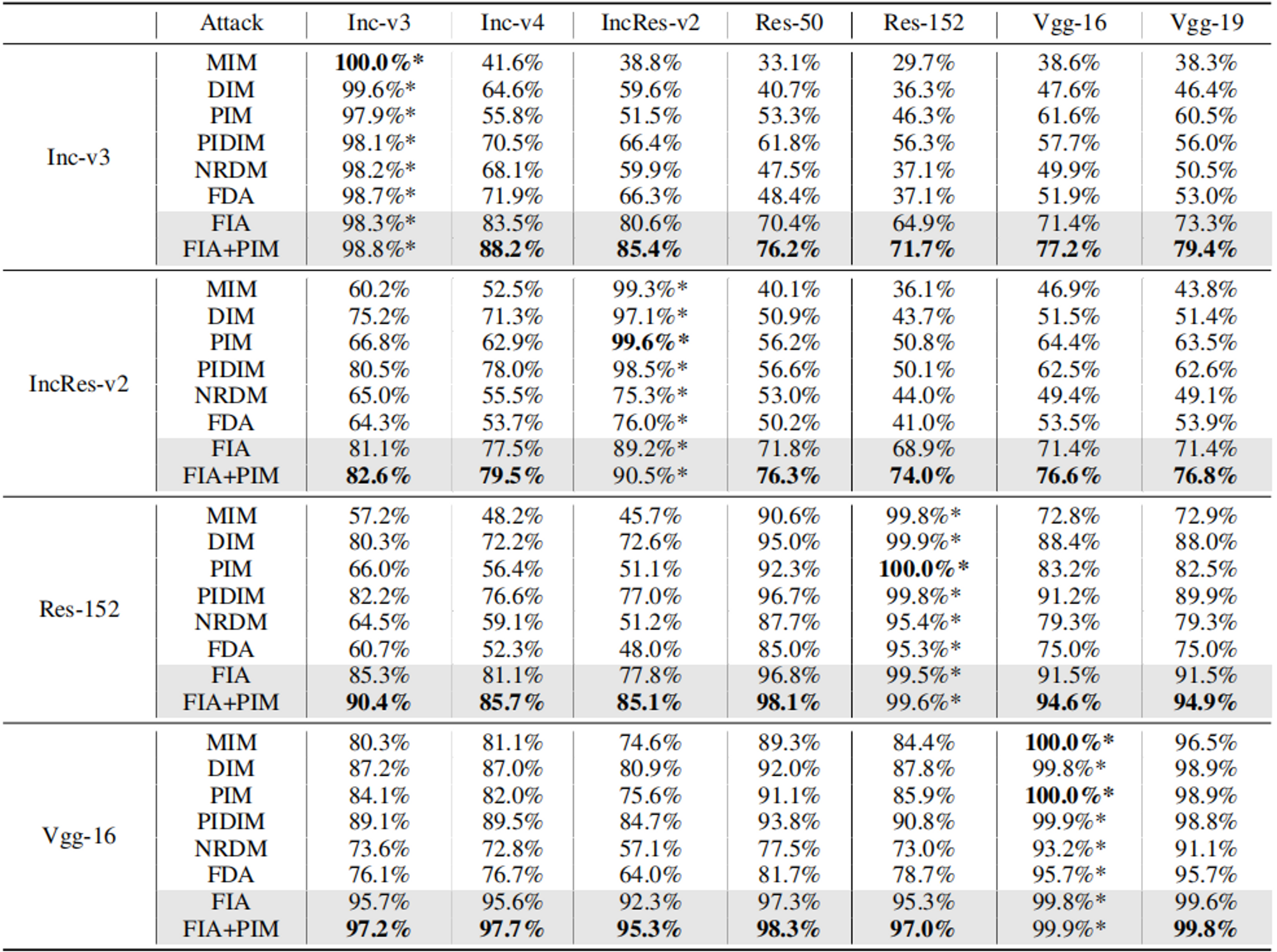
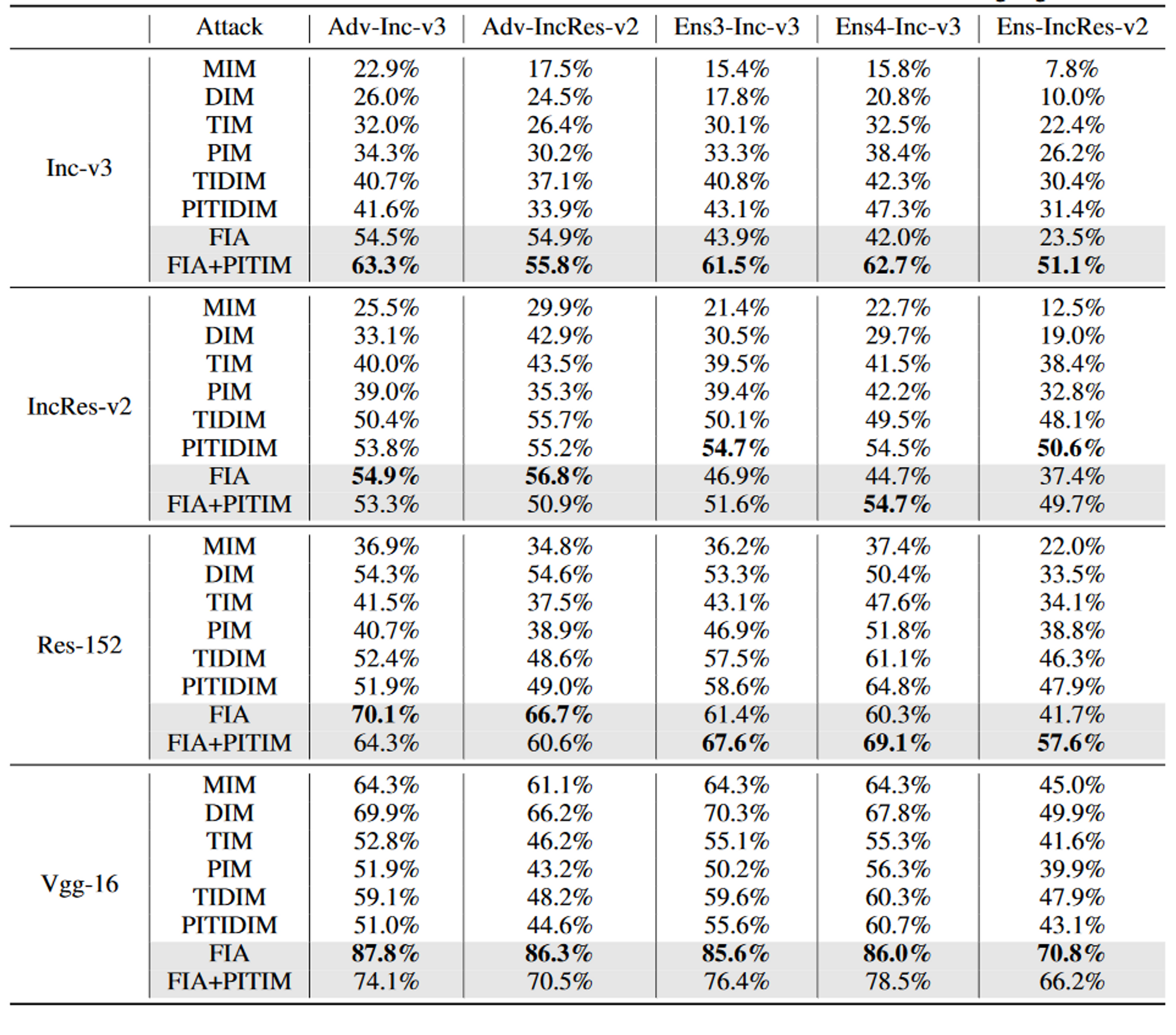
实验

• 下降率$P_d$：在影响成功率方面起着重要作用，而且这种影响在不同的目标模型中往往是一致的。一个较大的$P_d$（例如，0.5）会破坏图像的重要结构信息，从而显著降低成功率。因此，攻击正常训练模型的最佳$P_d$在0.2和0.3之间，而攻击防御模型的最佳$P_d$应该在0.1左右。
• 集合数$N$：较大的$N$往往产生较高的成功率，但会逐渐饱和。
• 最后我们确定了集成数$N=20$，正常训练模型的下降率$P_d=0.3$，以及防御模型的$P_d=0.1$。
• 选择中间层：特征层k的选择对特征级攻击有很大的影响，因为DNN的早期层（early layer）可能会构建一个通常是特定于数据的基本特征集，较进一步的层可能会对这些提取的特征进行处理，以最大化模型的分类精度，使这些特征进行处理，以最大化模型的分类精度，使这些特征成为特定于模型的。因此早期层没有学习到真正类别的显著特征和语义概念，而后期层是特定于模型的，在可迁移攻击中应该避开。相比之下，中间层（middle layer）具有良好的分类表示，并且它们与模型架构的相关性不高，因此中间层是为了更好的可迁移性而被攻击的最佳选择。