[人工智能]n-Queens的多种算法题解
相关叨叨:8皇后问题与n皇后问题
八皇后问题(英文:Eight
queens),是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。
问题表述为:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
下图是八皇后问题的一个解,可以用向量表示为:[f, d, g, a, h, b, e,
c],分别表示每行的皇后位置(列号)。 
实验拟题来自于 中国海洋大学 人工智能先导实践 lab03:比特匠心&模拟退火 -by 徐建良
n-queens多种解题方法思路
回溯与8皇后
“回溯法(back
tracking)(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。“
就是说,回溯法可以理解为通过选择不同的岔路口寻找目的地,一个岔路口一个岔路口的去尝试找到目的地。如果走错了路,继续返回来找到岔路口的另一条路,直到找到目的地。
而对于解决八皇后问题,以深度优先的回溯法作为最基础的思路,有如下应用:
step1. 尝试先放置第一枚皇后,被涂黑的地方是不能放皇后
 step2. 第二行的皇后只能放在第三格或第四格,比方我们放第三格,则:
step2. 第二行的皇后只能放在第三格或第四格,比方我们放第三格,则:
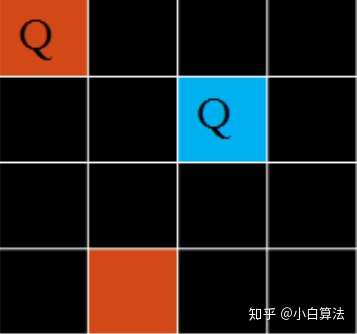 step3.
可以看到再难以放下第三个皇后,此时我们就要用到回溯算法了。我们把第二个皇后更改位置,此时我们能放下第三枚皇后了。
step3.
可以看到再难以放下第三个皇后,此时我们就要用到回溯算法了。我们把第二个皇后更改位置,此时我们能放下第三枚皇后了。
 step4.
虽然是能放置第三个皇后,但是第四个皇后又无路可走了。返回上层调用(3号皇后),而3号也别无可去,继续回溯上层调用(2号),2号已然无路可去,继续回溯上层(1号),于是1号皇后改变位置如下,继续回溯。
step4.
虽然是能放置第三个皇后,但是第四个皇后又无路可走了。返回上层调用(3号皇后),而3号也别无可去,继续回溯上层调用(2号),2号已然无路可去,继续回溯上层(1号),于是1号皇后改变位置如下,继续回溯。
 以上内容引自 小白带你学---回溯算法(Back
Tracking) -知乎 @小白算法
以上内容引自 小白带你学---回溯算法(Back
Tracking) -知乎 @小白算法
下面我们就建立在这一最基础的算法思路上,运用不同的进阶算法解决N阶皇后问题,且不断优化。
利用哈希表降维进行初探
算法说明
这个题解仅仅是建立在对该问题的探索与思考上,并无“创新”抑或“优化”可言,基于最暴力且朴素的降维思路,不断尝试从中找出规律、再考虑优化。
### 二维哈希表 · 实现过程: 1.
建立二维数组,将棋盘布局通过数组模拟占位信息。其中另外通过开辟数组分别存储列冲突、左斜冲突、和右斜冲突的信息。
2. 设置回溯函数,统计该行下空余且不冲突可放置皇后的位置;
->更新并计算位置占用情况;
->若有空余位置,则从右起对每一位置依次进行回溯试探;
->进入下一行的试探,深度优先搜索正确解,只要遇到无空位可放置,则逐层向上回溯,至存在空位的行;
->依次对该行存在的可放置空位进行遍历试探,并对试探失败的空位进行排除;
->记录可行解的个数。 3. 回溯函数部分代码如下 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46void dfs2(int** hash, int rowp)
{
//注释略
int flag = 1;
if (rowp == n)
{
num++;
flag = 0;
}
else
for (int i = 0;i < n;i++)
{
if (hash[rowp][i] == 1)
break;
else if (i == n - 1 && hash[rowp][i] == 0)
flag = 0;
}
if (flag)
{
int** temp = new int* [n - rowp - 1];
for (int i = 0;i < n - rowp - 1;i++)
{
temp[i] = new int[n];
for (int j = 0;j < n;j++)
temp[i][j] = hash[rowp + i + 1][j];
}
for (int i = 0;i < n;i++)
if (hash[rowp][i])
{
hash[rowp][i] = 0;
for (int down = rowp + 1, l = i - 1, r = i + 1;down < n;down++, l--, r++)
{
if (l >= 0)
hash[down][l] = 0;
if (r < n)
hash[down][r] = 0;
hash[down][i] = 0;
}
dfs2(hash, rowp + 1);
for (int m = 0;m < n - rowp - 1;m++)
for (int h = 0;h < n;h++)
hash[rowp + m + 1][h] = temp[m][h];
}
}
}
一维哈希表
· 实现: 1.
为了减少内存压力,通过将二进制数的位运算与数组进行结合,用n个二进制数记录行中可放置位置,并将之存放在一维数组中;
2. 思路与上大致相同,不再赘述。 3. 代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49void dfs1(int* hash, int rowp)
{
//注释略
int flag = 1;
if (rowp == n)
{
num++;
flag = 0;
}
else
for (int i = 0;i < n;i++)
{
if (hash[rowp])
break;
else
flag = 0;
}
if (flag)
{
do
{
int p = hash[rowp] & -hash[rowp];
int position = log(p) / log(2);
/*int position = p == 1 ? 0 : pow(p, 0.5);*/
hash[rowp] -= p;
int* temp = new int[n - rowp - 1];
for (int i = 0;i < n - rowp - 1;i++)
temp[i] = hash[rowp + i + 1];
for (int down = rowp + 1, l = 1, r = 1;down < n;down++, l++, r++)
{
int left = 0, right = 0;
if (l < n - position)
left = left + p << l;
if (r <= position)
right = right + p >> r;
hash[down] = hash[down] & ~(left | right | p);
}
/*cout << rowp << endl;
for (int i = 0;i < n;i++)
cout << bitset<6>(hash[i]) << endl;*/
dfs1(hash, rowp + 1);
for (int m = 0;m < n - rowp - 1;m++)
for (int h = 0;h < n;h++)
hash[rowp + m + 1] = temp[m];
delete[]temp;
} while (hash[rowp]);
}
}
位运算解法(0维哈希表)
位运算
位运算与位运算符: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15unsigned int a = 60; //60 = 0011 1100
unsigned int b = 13; //13 = 0000 1101
int c = 0;
c = a & b; //12 = 0000 1100 按位与
cout << "Line 1 - Value of c is: " << c << endl;
c = a | b; //61 = 0011 1101 按位或
cout << "Line 2 - Value of c is: " << c << endl;
c = a ^ b; //49 = 0011 0001 异或
cout << "Line 3 - Value of c is: " << c << endl;
c = ~a; //-61 = 1100 0011 按位取反
cout << "Line 4 - Value of c is: " << c << endl;
c = a << 2; //240 = 1111 0000 位左移
cout << "Line 5 - Value of c is: " << c << endl;
c = a >> 2; //15 = 0000 1111 位右移
cout << "Line 6 - Value of c is: " << c << endl;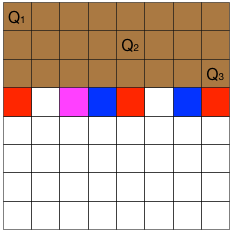 这个冲突其实有三种不同的情况,我们用三个变量
A,B,C
分别表示这三种不同的冲突。这三个变量都是一个八位的二进制数,这八位中,为
1 的表示有冲突,为 0 则表示没有冲突。 (1)与已放置的皇后处于同一列中:
我们用 A
表示这种冲突。例如在图中,第四行会有三个位置因为列攻击而不能再放置皇后(图中大红色方块),因此
A = 1000 1001。 (2)与已放置的皇后处于同一左斜(指向右下方)对角线中:
我们用 B
表示这种冲突。例如在图中,蓝色方块所表示的位置,分别是由于Q1和Q2的左斜对角线上的攻击而不能够放置新的皇后,
因此B = 0001 0010。 (3)与已放置的皇后处于同一右斜(指向右上方)对角线中:
我们用 C 表示这种冲突。例如图中粉色方块,是由 Q2
的右斜对角线的攻击造成的。因此 C = 0010 0000。 有了 A,B,C
三个变量,我们很容易求出当前行(第 4
行)中,有哪些位置是可以放置皇后的。这个变量我们用 D 来表示,我们可以写出
D = ~(A|B|C)。D中为 1 的那些位置则是我们可以放置皇后的位置。上图中,D =
0100 0100。
此时,我们有两个可能的放置皇后的位置,那么如何取出每个可能的位置呢?
这里有一个技巧。我们用 bit 表示可能的一个位置,使用 bit = D & (-D)
即可取出 D 中最右边的 1(LSB,Least Significant Bit)。例如 D = 0100
0100,则-D = 10111100(注意计算机中的数都是补码,-D = ~D + 1)。而bit =
D & (-D) = 0000 0100 取出了最右边的那个 1,代表在第 4 行第 6
列放置一个皇后。那么在此基础上,如何确定第 5 行的 A、B、C
的值呢?其实也很简单,对于表示列冲突的变量 A 来说,只要使用 A|bit
即可表示下一行的列冲突情况,对于 B,采用(B|bit)<<1,对于
C,采用(C|bit)>>1 即可表示下一行中,对角线冲突的情况。
上述算法的思路来自于 Backtracking
Algorithms in MCPL using Bit Patterns and Recursion -by
Martin Richards
(这个链接好像并不很稳定的样子,可以挂个梯子去看) 2. 代码如下:
这个冲突其实有三种不同的情况,我们用三个变量
A,B,C
分别表示这三种不同的冲突。这三个变量都是一个八位的二进制数,这八位中,为
1 的表示有冲突,为 0 则表示没有冲突。 (1)与已放置的皇后处于同一列中:
我们用 A
表示这种冲突。例如在图中,第四行会有三个位置因为列攻击而不能再放置皇后(图中大红色方块),因此
A = 1000 1001。 (2)与已放置的皇后处于同一左斜(指向右下方)对角线中:
我们用 B
表示这种冲突。例如在图中,蓝色方块所表示的位置,分别是由于Q1和Q2的左斜对角线上的攻击而不能够放置新的皇后,
因此B = 0001 0010。 (3)与已放置的皇后处于同一右斜(指向右上方)对角线中:
我们用 C 表示这种冲突。例如图中粉色方块,是由 Q2
的右斜对角线的攻击造成的。因此 C = 0010 0000。 有了 A,B,C
三个变量,我们很容易求出当前行(第 4
行)中,有哪些位置是可以放置皇后的。这个变量我们用 D 来表示,我们可以写出
D = ~(A|B|C)。D中为 1 的那些位置则是我们可以放置皇后的位置。上图中,D =
0100 0100。
此时,我们有两个可能的放置皇后的位置,那么如何取出每个可能的位置呢?
这里有一个技巧。我们用 bit 表示可能的一个位置,使用 bit = D & (-D)
即可取出 D 中最右边的 1(LSB,Least Significant Bit)。例如 D = 0100
0100,则-D = 10111100(注意计算机中的数都是补码,-D = ~D + 1)。而bit =
D & (-D) = 0000 0100 取出了最右边的那个 1,代表在第 4 行第 6
列放置一个皇后。那么在此基础上,如何确定第 5 行的 A、B、C
的值呢?其实也很简单,对于表示列冲突的变量 A 来说,只要使用 A|bit
即可表示下一行的列冲突情况,对于 B,采用(B|bit)<<1,对于
C,采用(C|bit)>>1 即可表示下一行中,对角线冲突的情况。
上述算法的思路来自于 Backtracking
Algorithms in MCPL using Bit Patterns and Recursion -by
Martin Richards
(这个链接好像并不很稳定的样子,可以挂个梯子去看) 2. 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29void dfs0(int hash,int B,int C)
{
//B左斜冲突
//C右斜冲突
int flag = 1;
//由于同列冲突的条件限定,且棋盘行数与列数相等
//若想在每一列都放置皇后,则皇后不可能在同列,同时满足每一列都有皇后
//因而可通过判断是否满足每一列都有皇后的条件来判断是否达成最终效果
//hash记录列冲突
//当hash==n,即所有每一列都放置了皇后时,结束本轮试探并计数
if (hash==n)
flag = 0;
if (flag)
{
//设置回溯记忆点rememtemp
//若rememtemp==0时,即该行无位置可供放置,结束试探并开始回溯
int rememtemp = n & ~(B | C | hash); //初始继承上一行中的放置情况
while (rememtemp)
{
//定义A表示同列冲突,且其列位置会直接被继承到该行后的各行中
int A = rememtemp & -rememtemp; //取当前行中最右一个可放置皇后的位置
rememtemp -= A; //在记忆点中将A位置设置为0
//左斜冲突与右斜冲突在继承上一行的冲突情况同时,分别通过对该A位置的左移与右移进行对下一行冲突的更新
//对hash更新列冲突情况
dfs0(hash | A, (B | A) << 1, (C | A) >> 1); //进入下一行
}
}
else num++;
}
 ###
小结
利用位运算对n-queens问题可行解的数量进行统计,其延续了上述通过哈希表的思路,但代码更为简洁、运行速度更快、占用空间更小。唯一比较困难的是对于单一的二进制变量来储存整个棋盘的空位更新信息,在向下试探过程中容易忽略对当前行的“存档”,而在回溯过程中又容易忘记“读档”,而导致信息混乱。这个问题的解决则是在每次递归之前设置一个存档变量,将当前的数据存储之后再进行向下的试探,因而保证了在每一层的回溯过程中会自动读取上次所记录的数据。
下图是1-27阶问题的所有可行解:
###
小结
利用位运算对n-queens问题可行解的数量进行统计,其延续了上述通过哈希表的思路,但代码更为简洁、运行速度更快、占用空间更小。唯一比较困难的是对于单一的二进制变量来储存整个棋盘的空位更新信息,在向下试探过程中容易忽略对当前行的“存档”,而在回溯过程中又容易忘记“读档”,而导致信息混乱。这个问题的解决则是在每次递归之前设置一个存档变量,将当前的数据存储之后再进行向下的试探,因而保证了在每一层的回溯过程中会自动读取上次所记录的数据。
下图是1-27阶问题的所有可行解: 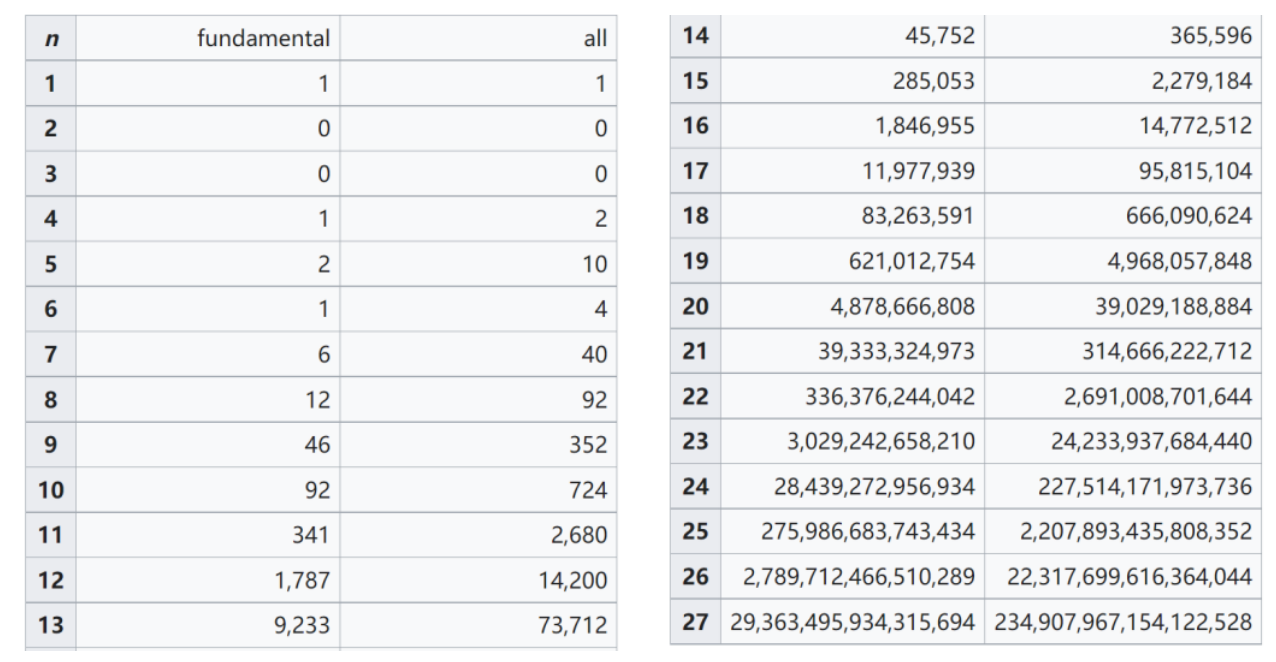 对于该图中的分布状态的总结与思考,又引出了下文新的算法——多项式时间算法。
对于该图中的分布状态的总结与思考,又引出了下文新的算法——多项式时间算法。
N皇后的多项式时间算法
算法说明
本算法来自于A Polynomial Time Algorithm for the N-Queens Problem -by Rok Sosic & Jun Gu (这个链接好像并不很稳定的样子,可以挂个梯子去看) 在 1990 年首先提出。其灵感来源于对n阶可行解数量的考察,可以得出:可行解数量众多且均匀分布于整个状态空间 (棋盘上皇后的所有可能的 n!个排列)中。 思路简述: 通过一维数组将行数与该行对应皇后的列位置建立映射; ->随机打乱并保证每行皇后不在同一列; ->遍历判断皇后i或皇后j是否存在对角线冲突; ->若冲突,则试探交换两行皇后的位置; ->判断交换后,全局冲突(评估值)是否减少,若减少则确定交换并使操作数自增记录,否则不交换且不记录; ->若都不冲突则不操作; ->遍历,知道操作数为0; ->判断调整后全局是否存在冲突,若存在则打乱重来(重启); ->输出该解。
如下图是原论文中关于算法思路的说明(部分): .png)
此算法只是用于寻找并输出任一可行解,而不作为计算可行解总数的算法。
代码实现
代码实现如下(虽然感觉我写的怪怪的): 1. 评估函数: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26//评估函数,计算当前棋盘下的冲突数,作为评估值
int Conflicts(int* Board)
{
/*cout << "c" << endl;
for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
int Conf = 0;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
//对角线冲突数
if (abs(j - i) == abs(Board[i] - Board[j]))
Conf++;
// 列冲突数
if (Board[i] == Board[j])
Conf++;
}
}
/*cout << Conf<<endl;*/
return Conf;
}
单个皇后局部对角线冲突计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//单个皇后局部对角线冲突
int Attacked(int *Board,int row)
{
/*for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
int Att = 0;
for(int i=row+1;i<n;i++)
if (abs(row - i) == abs(Board[i] - Board[row]))
Att++;
/*cout << Att<<endl;*/
return Att;
}取解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59void Heuristic(int* Board)
{
int swaps_performed = 0; //设定计步器
int* Current = new int[n]; //设定当前棋盘
int* Next = new int[n]; //设定试探棋盘
for (int i = 0;i < n;i++)
{
Current[i] = Board[i];
Next[i] = Board[i];
}
do {
swaps_performed = 0; //重计
for(int i=0;i<n;i++)
for (int j = i + 1;j < n;j++)
{
if (Attacked(Current, i) || Attacked(Current, j)) //if queeni is attacked or queenj is attacked
{
Next[i] = Current[j];
Next[j] = Current[i];
if (Conflicts(Next) < Conflicts(Current)) //if swap(queeni,queenj) reduces collisions
{
Current[i] = Next[i];
Current[j] = Next[j];
swaps_performed++;
/*cout << "?" << endl;*/
/*for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
}
else {
Next[i] = Current[i];
Next[j] = Current[j];
}
}
}
if (Conflicts(Current)) //检查是否获得解,若未获得解则打乱重来
{
srand((unsigned)time(0));
for (int i = 0;i < n;i++)
{
int j = rand() % n;
int temp = Current[i];
Current[i] = Current[j];
Current[j] = temp;
}
swaps_performed = 1;
}
} while (swaps_performed);
for (int i = 0;i < n;i++)
Board[i] = Current[i];
delete[]Next;
delete[]Current;
}多项式时间测试主函数:
结果展示(14皇后为例):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51void Polyn()
{
//Board[n]的值为棋盘第n行放置皇后的列位置
int* Board = new int[n];
for (int i = 0;i < n;i++)
Board[i] = i;
srand((unsigned)time(0));
for (int i = 0;i < n;i++) //保证不放在同列
{
int j = rand() % n;
int temp = Board[i];
Board[i] = Board[j];
Board[j] = temp;
}
/*for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
Heuristic(Board);
//输出解
for (int i = 0;i < n;i++)
{
for (int j = 0;j < n;j++)
{
cout << "+---";
if (j == n - 1)
cout << "+" << endl;
}
for (int j = 0;j < n;j++)
{
cout << "|";
if (Board[i] == j)
cout << " Q ";
else
cout << " # ";
if (j == n - 1)
cout << "|" << endl;
}
if (i == n - 1)
{
for (int j = 0;j < n;j++)
{
cout << "+---";
if (j == n - 1)
cout << "+" << endl;
}
}
}
}
小结:
在编写过程中,感觉有些熟悉,有点随机重启爬山的味道,怀疑是不是自己并没有很好地利用好原作者的多项式时间算法思路)因为在实现过程中会出现自动跳出局域最优解(而可能并未达到全局最优),因而出现错误的结果,遂在完全照搬论文中伪代码的内容同时,增添了随机重启的部分,来确保最终结果为全局最优而非仅仅的局部最优。 我在这里的处理似乎并不是一个最合适的弥补策略,可以说并未很好地遵照多项式时间算法的巧妙设计。后续(或许很有可能不会)再返回来好好参悟一下算法来源的论文。 而面对上述提到的局部最优解的跳出,下文将会由此展示一个巧妙解决局部困死问题/提高效率的算法。
模拟退火算法在N皇后问题的运用
模拟退火很好地解决了局部困死地问题,因为它在运行过程中会对微小变动进行一定程度上的接受,即使这个微小变动所得到的最终解并不是我们想要的解,正是这种设定提高了执行效率。 此算法只是用于寻找并输出任一可行解,而不作为计算可行解总数的算法。
算法说明
模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。
这里的“一定的概率”的计算参考了金属冶炼的退火过程,这也是模拟退火算法名称的由来。将温度T当作控制参数,目标函数值f视为内能E,而固体在某温度T时的一个状态对应一个解[公式],然后算法试图随着控制参数T的降低,使目标函数f(内能E)也逐渐降低,直至趋于全局最小值(退火中低温时的最低能量状态),就像金属退火过程一样。
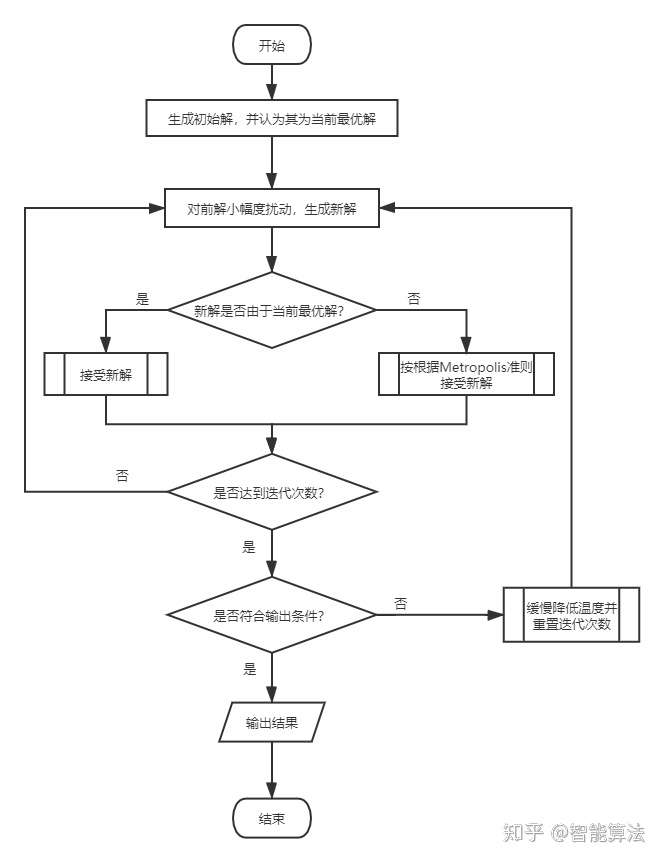 其中有几个需要注意的点: ·
初始点的选取对算法结果有一定的影响,最好是多次运行对结果进行综合判断。 ·
在算法运行初期,温度下降快,避免接受过多的差结果。当运行时间增加,温度下降减缓,以便于更快稳定结果。
·
当迭代次数增加到一定次数时,结果可能已经达到稳定,但是距离算法结束还有一段时间。在设计程序时应该加入适当的输出条件,满足输出条件即可结束程序。
其中有几个需要注意的点: ·
初始点的选取对算法结果有一定的影响,最好是多次运行对结果进行综合判断。 ·
在算法运行初期,温度下降快,避免接受过多的差结果。当运行时间增加,温度下降减缓,以便于更快稳定结果。
·
当迭代次数增加到一定次数时,结果可能已经达到稳定,但是距离算法结束还有一段时间。在设计程序时应该加入适当的输出条件,满足输出条件即可结束程序。
以上内容来自 模拟退火算法详解 -知乎 @智能算法
思路简述: 通过一维数组将行数与该行对应皇后的列位置建立映射; ->设定初始温度且足够大,设定最小温度且一定小,设定退火速率; ->以行为单位遍历调整皇后位置,并计算调整前后的冲突值的差; ->若能量差小于0,则证明修改后的评估值耕地,在一定概率下接收评估值降低的修改,且使这个概率不知逐渐减小;否则直接接受调整; ->逐渐降温确保在未获得最优解时跳出局部最低温; ->直至调整到获得全局最低温结束; ->输出该解。
代码实现
代码实现如下: 1. 评估函数(与多项式时间算法的全局冲突数函数一样)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25int Conflicts(int* Board)
{
/*cout << "c" << endl;
for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
int Conf = 0;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
//对角线冲突数
if (abs(j - i) == abs(Board[i] - Board[j]))
Conf++;
// 列冲突数
if (Board[i] == Board[j])
Conf++;
}
}
/*cout << Conf<<endl;*/
return Conf;
}
退火调整:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36int* proper(int* Board, int row)
{
double T = 100.0; //设定初始温度且足够大
double Tmin = 1.0; //设定最小温度且一定小
double Rate = 0.8; //退火速率
int* Current = new int [n]; //记录当前棋盘放置情况
int* Next = new int [n]; //记录修改后棋盘放置情况
for (int i = 0;i < n;i++)
{
Current[i] = Board[i];
Next[i] = Board[i];
}
while (T > Tmin) //开始退火
{
for (int p = 0;p < n;p++) //遍历修改
{
Next[row] = p;
double dE = Conflicts(Next) - Conflicts(Current); //计算能量差
//若能量差小于0,则证明修改后的评估值更低
//在一定概率下接受评估值降低的修改,且使这个概率值逐渐减小
if (dE <= 0 || (exp((-1) * dE / T) > rand() % 100 * 1.0 / 10))
Current[row] = Next[row];
/*for (int i = 0;i < n;i++)
{
cout << Current[i];
if (i == n - 1)
cout << endl;
}*/
}
T *= Rate; //降温
}
delete[]Next;
Board[row] = Current[row];
delete[]Current;
return Board;
}模拟退火测试主函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58void Simul()
{
//Board[n]的值为棋盘第n行放置皇后的列位置
int* Board = new int[n];
for (int i = 0;i < n;i++)
Board[i] = i;
srand((unsigned)time(0));
for (int i = 0;i < n;i++) //保证不放在同列
{
int j = rand() % n;
int temp = Board[i];
Board[i] = Board[j];
Board[j] = temp;
}
/*for (int i = 0;i < n;i++)
{
cout << Board[i];
if (i == n - 1)
cout << endl;
}*/
int row = 0,step=0;
while (Conflicts(Board))
{
if (row == n) //重置
row = 0;
Board = proper(Board, row++); //修改第row行皇后放置位置
/*cout << row;*/
}
//输出解
for (int i = 0;i < n;i++)
{
for (int j = 0;j < n;j++)
{
cout << "+---";
if (j == n - 1)
cout << "+" << endl;
}
for (int j = 0;j < n;j++)
{
cout << "|";
if (Board[i] == j)
cout << " Q ";
else
cout << " # ";
if (j == n - 1)
cout << "|" << endl;
}
if (i == n-1)
{
for (int j = 0;j < n;j++)
{
cout << "+---";
if (j == n - 1)
cout << "+" << endl;
}
}
}
}运行结果: 与上无差,不做赘述。
小结
经过对N皇后问题的不断深入探索(主要依赖于牛批前辈们的不同算法的提出),模拟退火用于寻找并输出n阶任一可行解,较好地解决了暴力遍历算法所导致的内存占用过大的问题/耗时过长效率低的问题,同时解决了多项式算法局部困死的问题,对该问题的不同算法探索到此为止(事实上是因为实验布置的内容要求到此为止)。
篇末BB
N-Queens/N皇后/无论怎么称呼的这一人工智能问题,属实经典,且解法众多,包括但远不限于如上所展示的 位运算/多项式时间算法/模拟退火算法 的经典算法,甚至如用爬山算法也将是很好的解题思路。对于人工智能,算法优化是其最关键的部分,面对庞大计算量,能否使程序语句更加精炼/占用内存尽可能少/运行速度更快,决定了你的人工是否足够智能。
(反正对于这一灵活度极高的问题上,我搜索且浏览了很多资料和文献才逐步探索出最优的算法,一圈子下来只是觉得自己是一人工智障)

![[日常] v我50来点文子哥的保研经历](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/1728380966977.png)
![[计算机网络]可靠传输协议迭代设计-来跟👴握个手](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/v2-479a601f5f20bca19018dddb68c0d708_720w.jpg)
![[文献阅读]增强对抗可迁移性的自适应模型集成对抗攻击-AdaEA](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/v2-435ccdae8ee452e7f5b7458b0e47683b_720w.webp)
![[文献阅读]侵蚀攻击:利用侵蚀改善对抗样本可迁移性-ErosionAtt](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/v2-39fe950ae3583892941537bc447c4e72_b.jpg)
![[文献阅读]基于平均梯度的对抗攻击-I-FAGSM](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/image-20230813230657904.png)