[文献阅读]通过对抗统计一致性规避深度伪造检测器-StatAttack

Information

论文位置：[2304.11670] Evading DeepFake Detectors via Adversarial Statistical Consistency

日期：2023-04-23

关键词：Adversarial Attack, DeepFake

出处：CVPR 2023

摘要

深度伪造检测技术通常依赖于检测自然（真实）图像和深度伪造生成图像在空域和频域的统计差异。

本论文提出显式地最小化统计差异来规避最先进的深度伪造检测器——针对深度伪造检测器的统计一致性攻击（StatAttack）：

1. 选取几种统计敏感的自然退化（曝光度、模糊度、噪声），并将其以对抗的方式添加到伪造图像中。
2. 自然图像和深度伪造图像之间的统计差异与两种图像之间的分布偏移正相关，本论文提出使用感知节点分布损失来指导不同退化的优化，因此，生成的对抗样本的特征分布接近更自然图像。
3. 将StatAttack扩展到MStat Attack，将单层退化依次扩展到多层退化，并利用损失联合调整组合权重。

介绍

深度伪造检测器容易受到对抗性攻击，这些攻击可以通过向假图像中注入扰动来绕过检测器。

以往的一些研究探讨了对抗样本的可迁移性，它是针对特定受害者模型设计的对抗样本攻击为同一任务训练的其他模型的能力。

不同的数据增强和预处理方法导致的网络架构和训练样本的变化，实现针对深度伪造检测器的可迁移攻击具有挑战性，这些差异往往导致在面对不同的深度伪造检测器时，基于典型攻击方法构造的对抗样本的可迁移性较差。

StatAttack选择三种统计敏感的自然退化，包括曝光、模糊和噪声，并以对抗的方式将他们添加到假图像中。真假图像集之间的统计差异与其分布偏移正相关。

本论文提出通过最小化伪造图像和自然图像的特征分布之间的距离来缓解这些差异。通过引入一种感知节点分布损失函数，有效地最小化了统计差异。

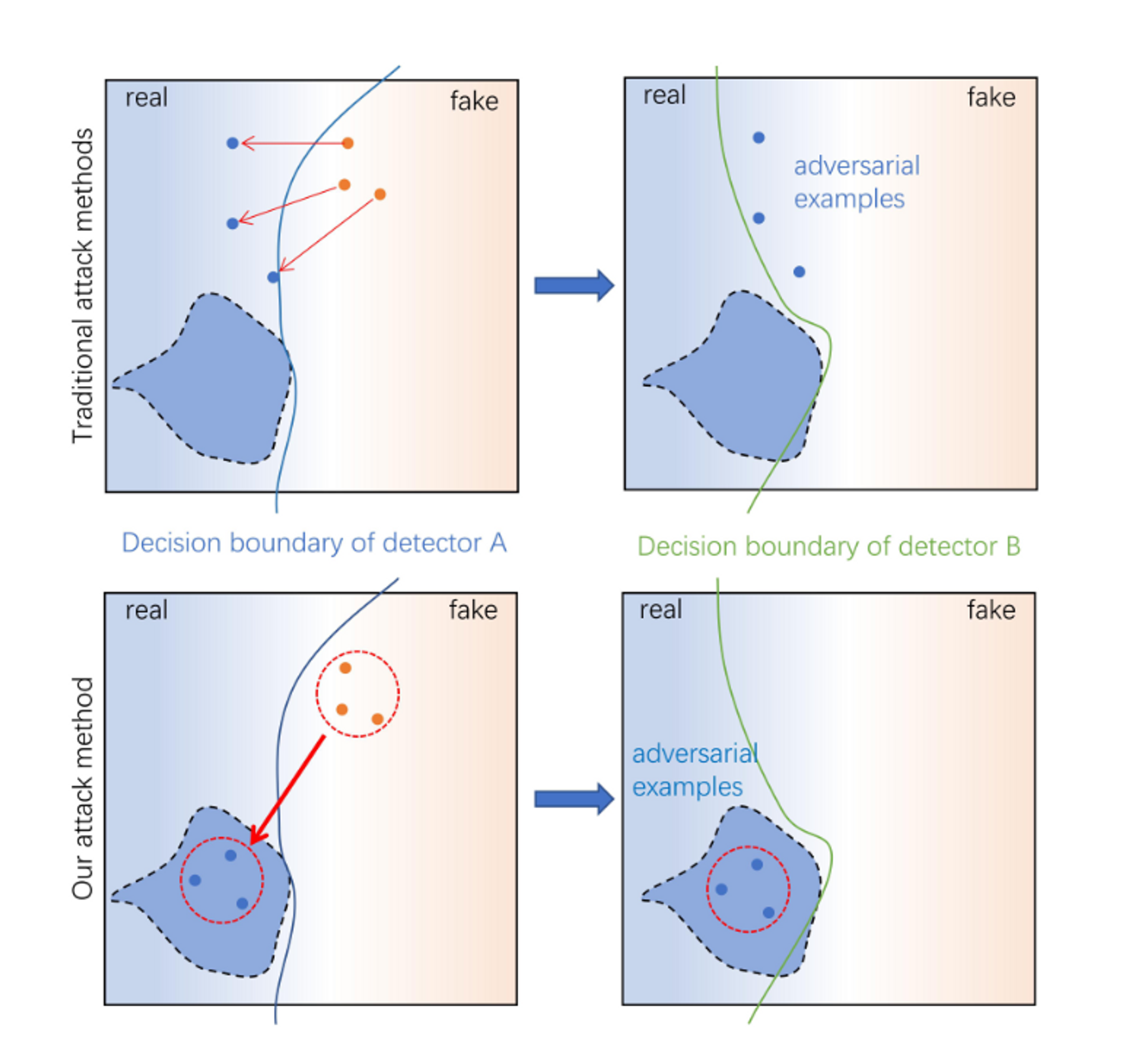
MStatAttack执行多层退化，并且可以在每个攻击步骤中动态调整不同层中每个退化的权重。

主要贡献

• 提出了一种新的基于自然退化的攻击方法StatAttack，可以通过最小化一个感知节点分布损失来填补真假图像之间的特征分布差异
• 提出了进一步的多层对应的MStatAttack，可以选择更有效的扰动组合并生成更自然的对抗样本

工作

统计学差异

几种检测方法解释了自然图像和伪造图像在频域和空间域的统计差异。

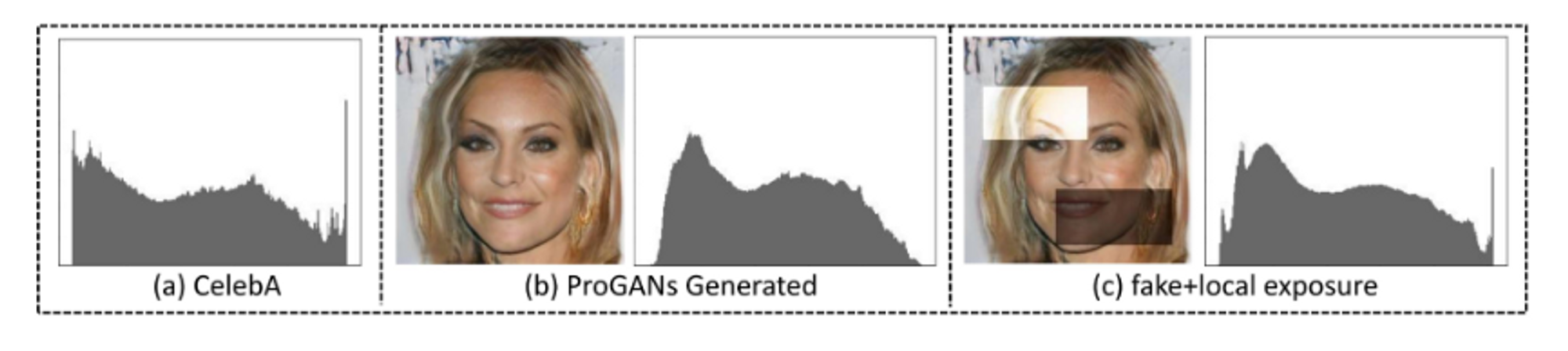
1. GAN网络架构和训练过程会导致GAN生成图像和自然图像之间的亮度统计差异。例如，一些GAN仅能生成强度值有限的图像，无法生成饱和和曝光不足的区域。

   

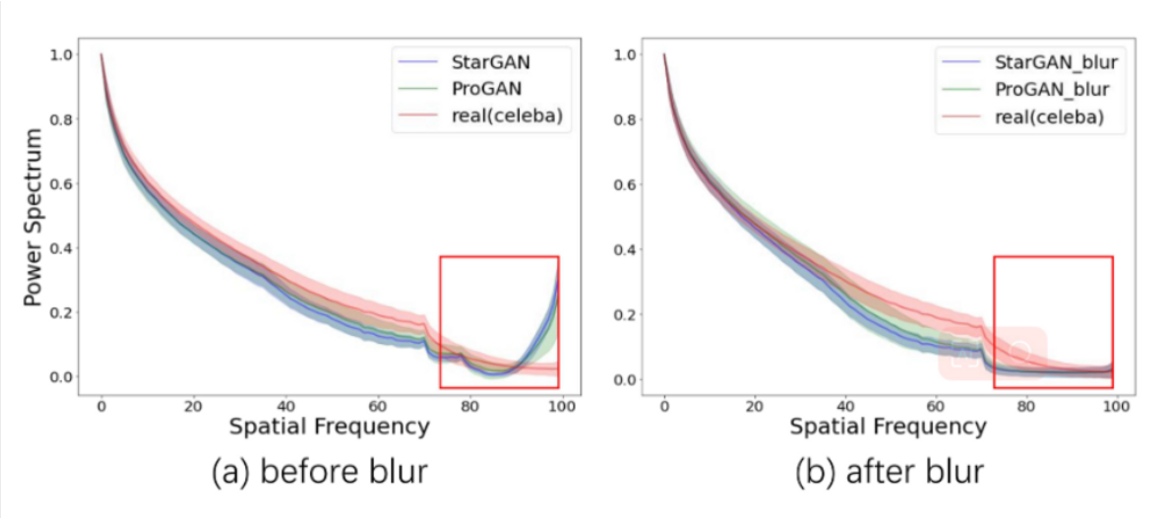
2. 自然图像和GAN生成图像在频域信息上的统计差异，揭示了高频成分的显著差异。

   

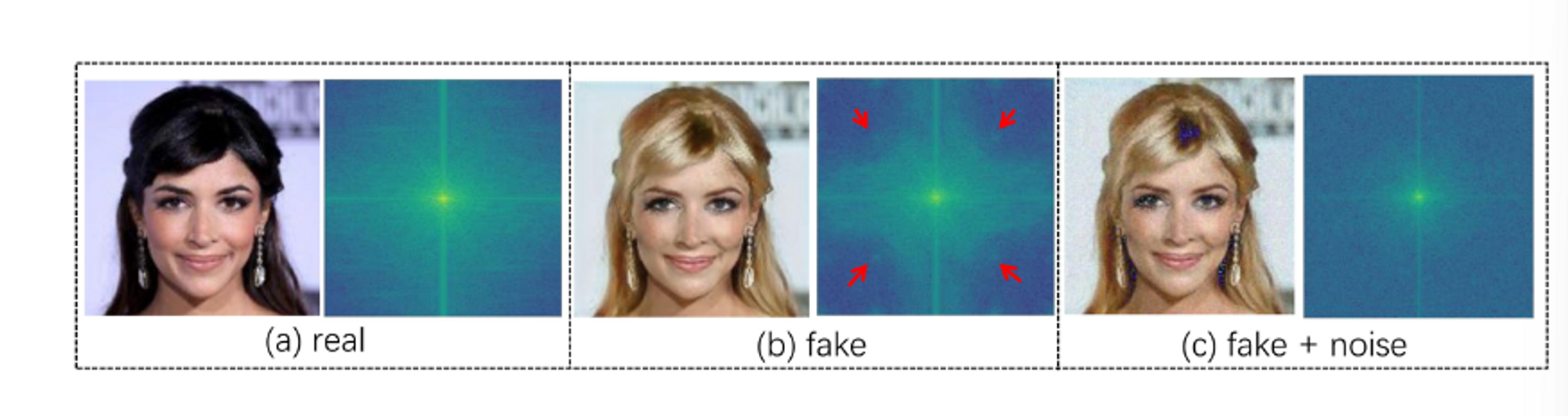
3. 通过直接观察GANs生成图像的频谱图发现了一些统计线索。他们的实验结果表明GANs不可避免地会在处理后的图像中留下规则的高频伪影。

   

统计一致性攻击(StatAttack)

统计敏感退化

1. 退化选择

   三种常见的能有效降低统计差异的自然退化：

   • 改变曝光。调整局部区域像素的亮度值可以改变伪造图像的亮度分布。如fig2。
   • 添加模糊。通过高斯低通滤波器滤除伪造图像中的高频成分，可以减小频域统计差异。如fig3。
   • 添加噪声。如fig4。通过加入随机噪声，伪造图像中的规则伪影被消除。

   值得注意的是，在图像中加入局部曝光不仅可以改变空间域的信息，还可以改变频率域的信息。此外，高斯滤波可以减少伪影图像中一些规则的高频伪影。

2. 自然的曝光对抗

   旨在将局部曝光注入到伪造图像中，使其亮度统计更接近自然图像。除此之外，由于自然曝光变化平滑，因此注入到伪造图像中的曝光也应该具有类似的（即图像中相邻像素具有相似的曝光值）性质。

   采用对抗曝光生成模型：由用于生成曝光的多项式模型和用于保持曝光自然度的平滑公式构成。

   • $P_e(\mathbf{X}^{fake})=log^{-1}(\tilde{\mathbf{X}}^{fake}+\tilde{\mathbf{E}})$，(1)
     • $\tilde{E}$：生成曝光的多项式模型
     • $\mathbf{X}^{fake}$：fake image
     • $\tilde{\cdot}$：对数运算

   为了保持曝光的自然性，对于多项式模型包含的两组参数$\mathbf{a}$和$φ$，我们通过在损失函数中加入平滑方程来约束其取值：

   • $S (a, φ) = −λa ||a||_2^2−λφ||▽φ||_2^2$，(2)

     超参数$λa$和$λφ$：调节对抗攻击用户平滑性之间的平衡。

3. 高斯模糊对抗

   对于一般的高斯模糊，在图像中不同位置使用的高斯核具有相同的值。为了以对抗的方式添加高斯模糊退化，我们提出将高斯核设计为可学习的对抗核。该方法允许在图像的不同位置自适应地应用对抗扰动。

   我们旨在学习一个标准差图$σ$，利用$σ_{x_i,y_i}$，计算第$i$个像素$H_i$的对抗高斯核如下：

   • $Hi(u, v) = \frac{1} {2π (σ{xi,y_i} )^2} exp(−\frac{ u^2 + v^2}{ 2π (σ{x_i,y_i} )^2})$，(3)
     • $σ_{x_i,y_i}$：高斯核在第$i$个像素位置的初始标准差
     • $u$和$v$表示高斯核内点到中心像素$(x_i,y_i)$的相对坐标

   利用对抗高斯核，对伪造图像进行模糊：

   • $P_b(\mathbf{X}^{fake}) = \sum \limits {i∈\mathcal{N} (i)} g(\mathbf{X}^{fake} i , k) ∗ \mathbf{H}_i$，(4)
     • $\mathcal{N}(i)$：$\mathbf{X}^{fake}$中所有像素
     • $g(\mathbf{X}^{fake},k)$：以第$i$个像素为中心，被包围在半径为$k$的高斯核内的区域
     • $*$：滤波操作运算符

   给生成的图像$Pb(\mathbf{X}^{fake})$一个与对抗相关的损失函数，并通过公式(4)最小化它得到${σ{x_i,y_i}}$和$\mathbf{H}_i$。随后，通过计算的高斯核对伪造图像施加像素级高斯模糊。

4. 噪声对抗

   • $P_n(\mathbf{X}^{fake}) = \mathbf{X}^{fake} + \mathbf{N}_a$，(5)
     • $\mathbf{N}_a$：与$\mathbf{X}^{fake}$大小相同的对抗噪声图。

   在每个攻击步骤中，我们通过最小化我们的对抗损失函数来生成对抗噪声，然后将其添加到每个fake image中。为了确保对抗噪声不会显著影响图像的质量，我们使用约束项对$\mathbf{N}_a$进行稀疏化。该约束项被纳入到最终的目标函数中。

5. StatAttack

   将上述扰动总结如下：

   • $P_θ(\mathbf{X}^{fake}) = P_n(P_b(P_e(\mathbf{X}^{fake})))$，(6)

     $P_θ(\mathbf{X}^{fake})$ 包含四组待优化参数${\mathbf{a},φ,σ,\mathbf{N}_a}$

感知节点分布统计一致性

给定一组真实图像和一组伪造图像，本论文研究了两个集合的统计差异与分布偏移之间的相关性，发现统计差异与两个集合之间的分布偏移正相关。

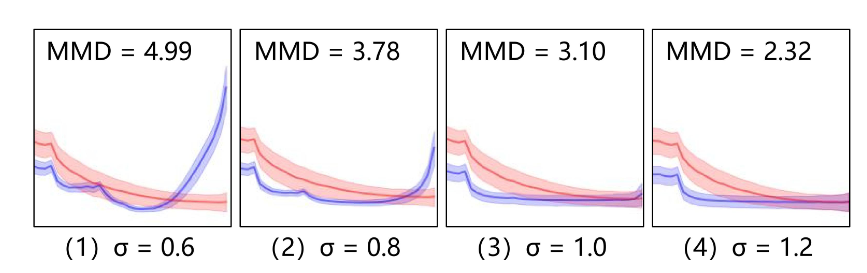
fig6.统计差异与自然图像集和伪造图像集的分布偏移之间的相关性。(1)-(4)展示了两组特征分布之间的功率谱和MMD值。蓝色曲线表示GAN生成图像的高频部分，红色曲线代表自然图像的。使用不同高斯核$\sigma$的高斯模糊处理伪造图像，观察到随着高频统计差异的减小，MMD值也随之减小。

使用最大均值差异（MMD）来衡量过滤后的伪造图像与自然图像的特征分布之间的距离。增大$\sigma$可以降低伪造图像中的高频频谱，且MMD值随着统计差异的减小而减小。

1. 目标函数

   若生成的对抗样本被分类为相反的类，则认为对二分类器的攻击是成功的。目标函数：

   • $\mathop{argmin} \limits{a,φ,σ,\mathbf{N}a} J{MMD}( Pθ (\mathcal{X}^{fake}) , \mathcal{X}^{real}) + S(\mathbf{a}, φ), \newline subject\ to\ ∥N_a∥_p ≤ \epsilon$，(7)
     • $\mathcal{X}$：图像集
     • $J_{MMD}(\cdot)$：在某个检测器层中两个特征分布之间的MMD值。

   通过目标函数计算曝光对抗、高斯模糊对抗和噪声对抗的参数。

2. 算法

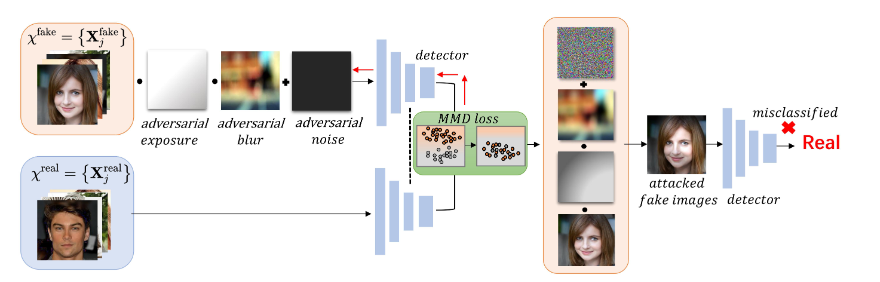
   初始化3个扰动参数${\mathbf{a},φ,σ,\mathbf{N}_a}$，并将其添加到伪造图像中。接下来，在每个基于DNN的检测器模型中收集自然图像和伪造图像在全局池化层上的特征分布，并计算它们的MMD值。为了优化扰动参数，我们使用符号梯度下降来最小化方程(7)。最后，将${\mathbf{a},φ,σ,\mathbf{N}_a}$的优化值应用于原始伪造图像，从而生成对抗伪造图像。

多层Stat攻击（MAtatAttack）

在图像中反复添加对抗扰动可能会提高攻击的成功率。因此我们进一步将StatAttack扩展到MStatAttack，依次将单层退化扩展到多层退化，并使用损失来联合调整组合权重。

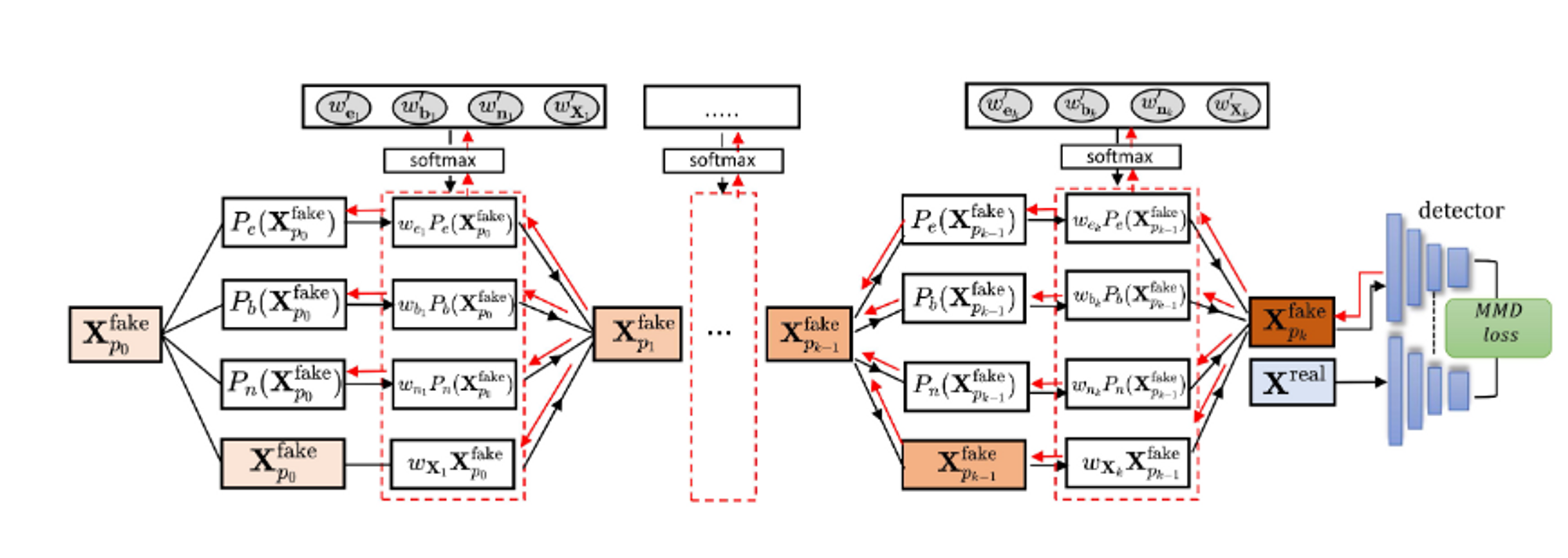
如fig7所示，MStatAttack使用多层来处理输入。在第k层，MStatAttack取第(k-1)层的输出，记为$\mathbf{X}^{fake}{p{k-1}}$，并行应用3种退化对抗（$e、b、n$）；然后，我们维护四个权重（$w’{e_k}、w’{bk}、w’{n_k}、w’{\mathbf{X}k}$）以混合$\mathbf{X}^{fake}{p{k-1}}$及其3个扰动版本，获取第k层的输出。为了保证四个权重之和等于1，我们将它们馈送到softmax层，得到（$w{e_k}、w{bk}、w{nk}、w{\mathbf{X}_k}$）。各层扰动可写作：

• $X^{fake}{p_k} = w{ek} P_e(\mathbf{X}^{fake}{ p{k−1}})+w{bk} P_b(\mathbf{X}^{fake} {p{k−1}} ) + w{nk} P_n(\mathbf{X}^{fake}{ p{k−1}} ) + w{\mathbf{X}k} \mathbf{X}^{fake}{ p_{k−1}} , n ≥ 1$，(8)

  $\mathbf{X}^{fake}_{p_k}$：第k层生成的对抗样本

在优化过程中，基于损失函数对原始权重和所有退化参数进行联合优化。sofmax层确保更新后的权重相加为1，防止图像混合过程种的强度溢出。

除了自动选择合适的攻击策略（即扰动组合）外，MStatAttack还可以通过原始伪造图像中融入更多的成分来增强生成的对抗样本。

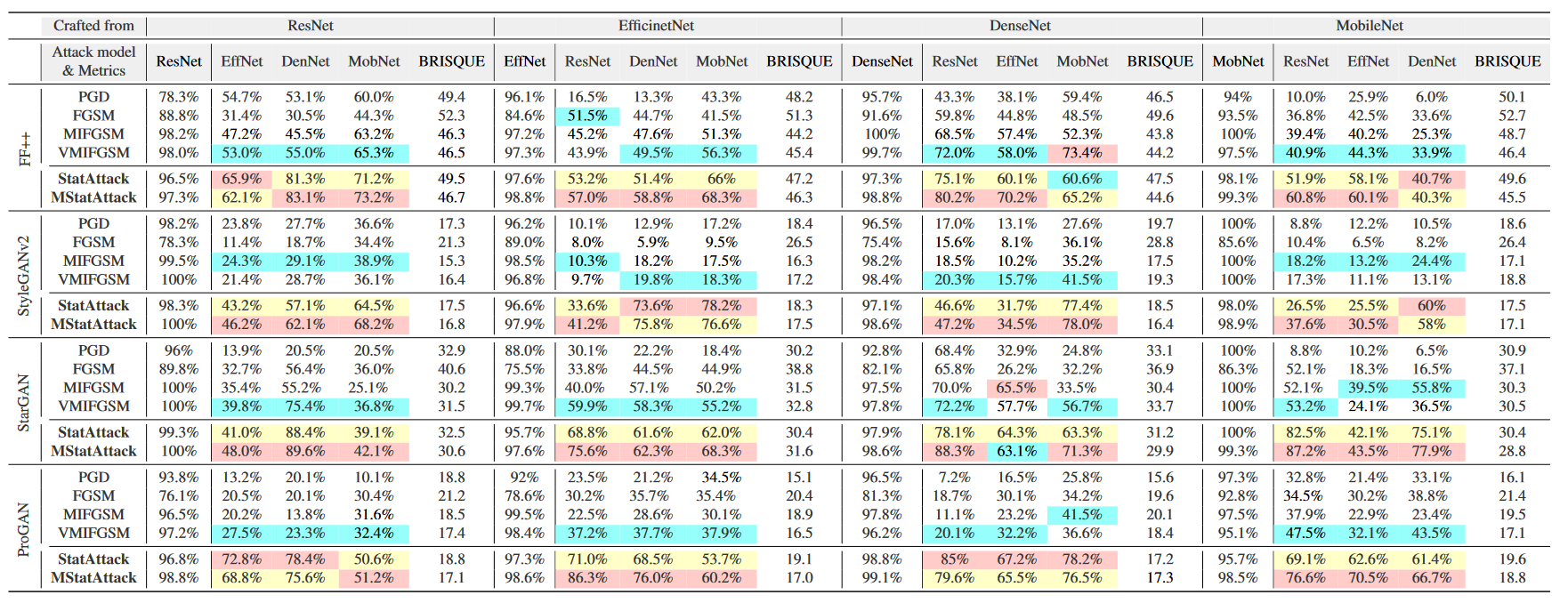
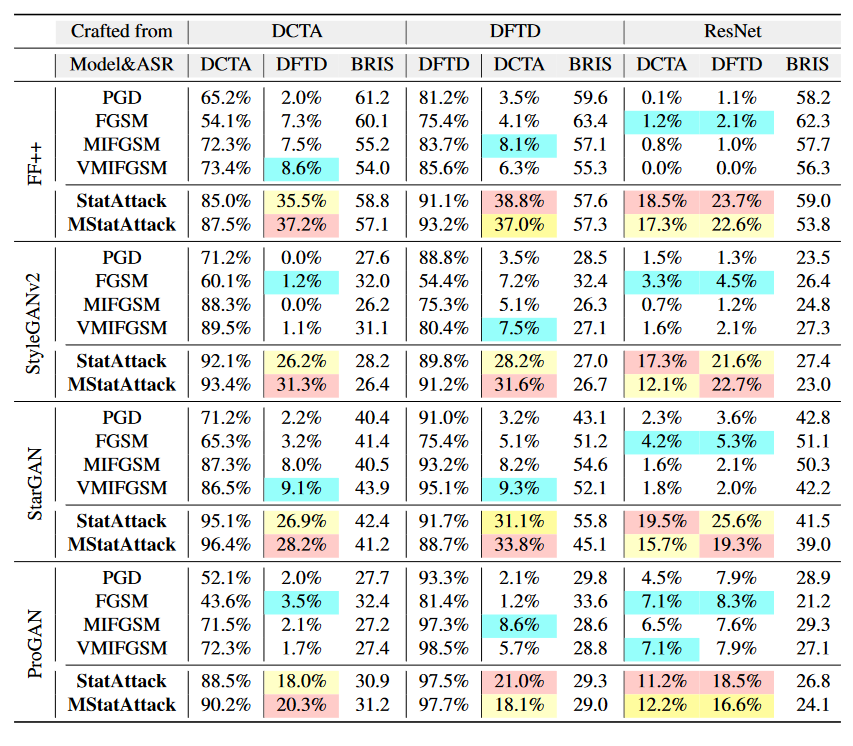
实验