[文献阅读]基于平均梯度的对抗攻击-I-FAGSM
Information
论文位置:Average gradient-based adversarial attack
日期:2023-03
关键词:Adversarial Attack, black-box attack, dynamic set of daversarial examples
出处:IEEE Trans. Multimedia
概要
本文提出了一种新的基于平均梯度的对抗攻击。在我们提出的方法中,通过利用过去每次迭代的梯度,在每次迭代中首先构建一个动态的对抗样本集,然后根据损失函数关于所构造的动态集和当前对抗样本中所有样本的梯度,可以计算出平均梯度,用于确定所添加的扰动。
与现有的对抗攻击不同,所提出的基于平均梯度的攻击通过一个动态的对抗样本集来优化添加的扰动,其中动态集的大小随着迭代次数的增加而增加。该方法具有良好的可扩展性,可以集成到大多数现有的基于梯度的攻击中。
背景
现有的数据增强策略大多是通过使用一些数字图像处理技术对输入样本进行转换来实现的,可以很容易地引入到上述基于梯度的攻击中。
基于平均梯度的攻击可以看作是基于高级梯度计算的攻击和基于数据增强的对抗攻击的结合。
首先,我们在基于梯度的对抗攻击中引入一个新的平均梯度项,它可以帮助稳定扰动的更新方向,避免陷入交叉的局部最优。
其次,不同于现有的数据增强策略,使用经典的数字图像处理奇数对输入样本进行变换,我们提出的方法使用过去迭代中获得的平均梯度对输入样本进行变换,从而形成对抗空间来增强算法的泛化能力。
贡献:
- 通过充分利用过去迭代中的梯度信息,在当前迭代中构建一个动态的对抗样本集,可以看作是一种新的数据增强策略。
- 通过结合损失函数关于动态集合中所有样本和当前对抗样本的梯度,可以计算出平均梯度项,可视为一种新的高级梯度计算策略。
- 所提出的平均梯度项具有良好的可扩展性,可以很容易地集成到大多数现有的基于梯度的攻击中,形成一系列新的强大的攻击,而不需要引入任何新的超参数。
- 本论文所提出的基于平均梯度的攻击能够取得较高的攻击成功率,生成的对抗样本表现出良好的可移植性。
研究方法
提出方案
设$x$为原始样本,$y$为与$x$相关的标签,$T$为迭代次数,$α$为小步长,$x_T^{adv}$为获得的对抗样本。$x_T^{adv}$是在原算例$x$(即$x_0^{adv}$)的基础上加入扰动后得到的。
改进梯度和数据增强是提高对抗样本可迁移性的两种主要策略。所提攻击可视为基于高级梯度计算的攻击的组合。在本论文的方案中,在每次迭代中首先构造一个动态的对抗样本集,这些样本实际上与输入样本非常相似,并用作数据增强样本。
然后,将损失函数关于当前示例和动态集中示例的平均梯度作为新的高级梯度项应用到我们的算法中。不失一般性,我们假设当前迭代为第$t$次迭代,待生成的动态集合用$S_t$表示。
定义1. 对抗样本的动态集合
动态的对抗实例集$S_t={\tilde{x}^{adv}_t[0],\tilde{x},\tilde{x}^{adv}_t[1],…,\tilde{x}^{adv}_t[t-1]}$由$t$个临时对抗>样本组成,由下式计算:
$\tilde{x}^{adv}t[i]=x^{adv}{t-1}+α·\frac{\bar{A_i}}{||\bar{A_i}||_1}$,(1)
- $\tilde{x}^{adv}_{t-1}$是在$(t-1)$次迭代中得到的对抗样本
- $\tilde{A_i}$是在第$i$次$(0≤i≤t-1)$次迭代中得到的平均梯度
如式(1)所示,对对抗样本${x}^{adv}_{t-1}$添加归一化平均梯度$\frac{\bar{A_i}}{||\bar{A_i}||_1}(0≤i≤t-1)$,可以得到由$t$个临时样本组成的动态集合$S_t={\tilde{x}^{adv}_t[0],\tilde{x},\tilde{x}^{adv}_t[1],…,\tilde{x}^{adv}_t[t-1]}$。通过充分利用过去每次迭代的梯度来构造对抗样本的动态集合,可视为一种新的数据增强策略。每次迭代生成的对抗样本的动态集合如图:
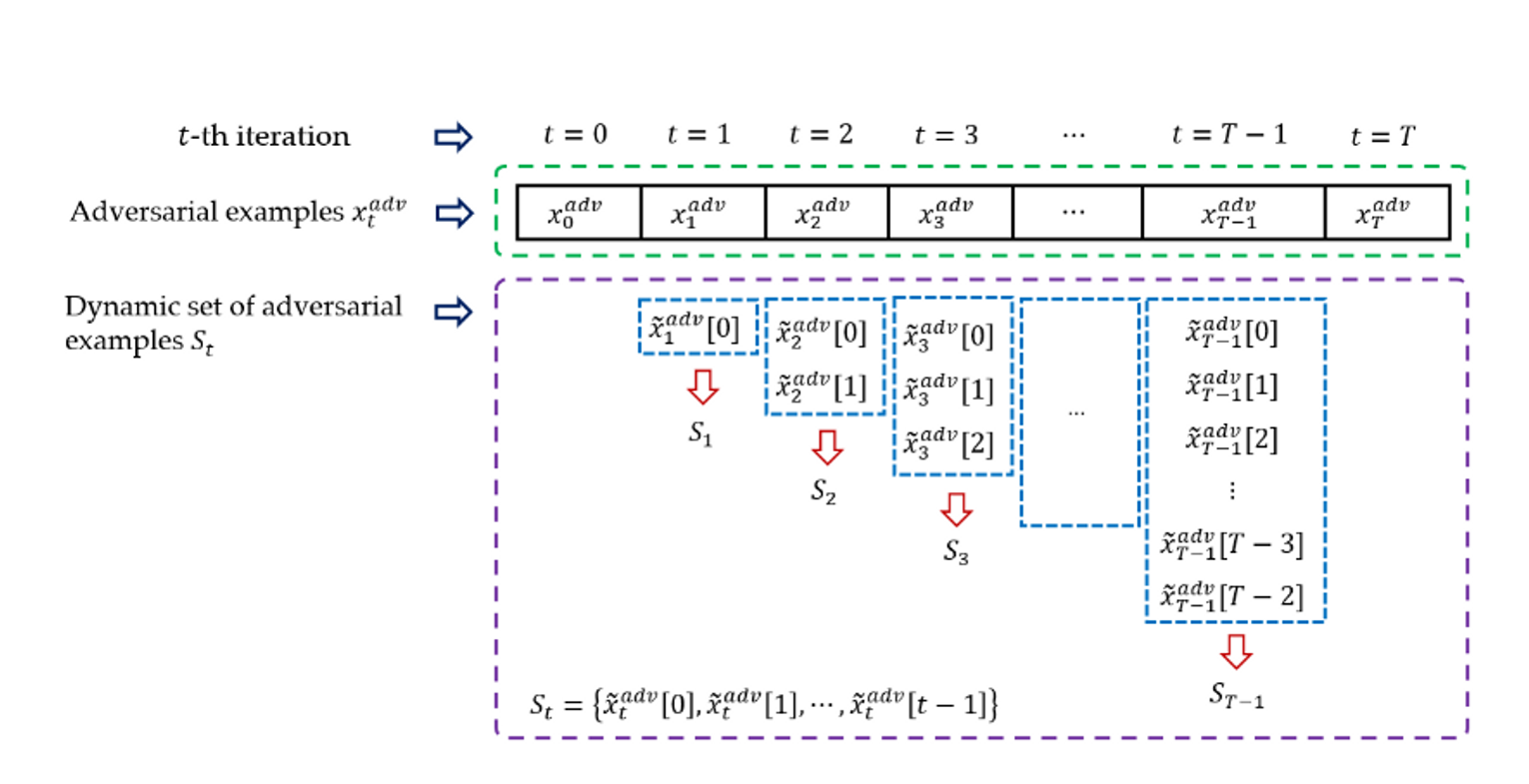
其中对抗样本(包括原始输入样本$x^{adv}0$),一些中间样本${x^{adv}_1,x^{adv}_2,…x^{adv}{T-1}}$和最终样本$x^{adv}T$和动态集(包括$S_0,S_1,…,S{T-1}$)分别包括在绿色虚线和紫色虚线框中。可以观察到在初级阶段($t=0$),动态集$S_0=\emptyset$,在第$t$次迭代中,动态集$S_t$中有$t$个临时对抗样本。
定义2. 平均梯度
如前所述,在第$t$次迭代中,存在$(t+1)$个对抗样本,即当前样本$x^{adv}t$和其他$t$个临时样本$\tilde{x}^{adv}_t[0],\tilde{x},\tilde{x}^{adv}_t[1],…,\tilde{x}^{adv}_t[t-1]$。损失函数关于当前示例$x^{adv}_t$和临时示例$\tilde x^{adv}_ti$的梯度分别用$\nabla{x^{adv}_t}L(x^{adv}_t,y)$和$\nabla*{\tilde x^{adv}_t}L(\tilde x^{adv}_t,y)$表示。
第$t$次迭代的平均梯度$\bar A_t$计算为下式:
$\bar At=\begin{cases}\nabla{x0^{adv}}L(x_0^{adv},y)&\text{t=0}\ \frac{1}{t+1}[\nabla{xt^{adv}}L(x^{adv}t,y)+\sum \limits{i=0}^{t-1}\nabla{\tilde x_t^{adv}[i]}L(\tilde x_t^{adv}[i],y)] &\text{t≥1}\end{cases}$,(2)
在第1次迭代($t=0$)中,由于没有临时对抗样本,且动态集合$S0=\emptyset$,因此平均梯度$\tilde{A0}$等于$\nabla{x_0^{adv}}L(x^{adv}_0,y)$。如式(2),随着迭代次数$T$的增加,越来越多的例子被考虑到计算平均梯度$A_t$。在实际应用中,融合更多示例的梯度一般可以提高泛化性。
对于如何在第$t$次迭代中获得对抗样本$x_{t+1}^{adv}$,由下式得出:
$g_{t+1}=\mu·g_t+\frac{\bar A_t}{||\bar A_t||_t}$,(3)
$x^{adv}_{t+1}=Clip^\epsilon_x {x^{adv}t+α·sign(g{t+1})}$,(4)
其中$g0=0$,$\bar A_t$为第$t$次迭代得到的平均梯度,$g_t$为迭代$t$时归一化平均梯度的累加,$μ$为衰减因子。在本论文方法中,首先对平均梯度$A_t$进行归一化,然后结合累加梯度$g_t$来更新梯度$g{t+1}$,如式(3)所示。最后,根据梯度$g{t+1}$可以生成式(14)所示的对抗样本$x^{adv}{t+1}$。可以看出,在本方案中,增加的扰动主要由归一化平均梯度的累加决定,这可以被认为时一种新的高级梯度计算策略。
MI-FAGSM算法

如图所示,在第$t$次迭代中生成$t$个临时样本,总共需要生成$\sum \limits{i=0}^{T-1}i$个临时样本才能得到最终的对抗样本$x_T^{adv}$,除了计算损失函数关于$T$个对抗样本(即$x^{adv}_0,x^{adv}_1,…,x^{adv}{T-1}$)的梯度外,还需要计算损失函数关于$\sum\limits{i=0}^{T-1}i$个临时样本的梯度。因此,生成对抗样本$x_T^{adv}$的梯度计算总数为$\sum \limits{i=1}^Ti$。一般而言,在基于梯度的攻击中,梯度计算次数是衡量攻击算法时间复杂度的主要因素。
延展性
与MI-FGSM相比,我们提出的方法将当前梯度$\nabla_{x^{adv}_t}L(x_t^{adv},y)$替换为平均梯度$\bar A_t$。
MI-FGSM:$g{t+1}=\mu·g_t+\frac{\nabla{x^{adv}_t}L(x^{adv}_t,y)}{||\nabla L(x^{adv}_t,y)||_1}$
MI-FAGSM:$g_{t+1}=\mu·g_t+\frac{\bar A_t}{||\bar A_t||_1}$
提出的平均梯度项可以很容易地引入到基于梯度的对抗攻击中,即在MI-FGSM、NI-FGSM、PI-FGSM引入平均梯度项,得到MI-FAGSM、NI-FAGSM、PI-FAGSM。
本算法中引入的平均梯度项不需要任何新的超参数,因而得到的方法(MI-FAGSM等)可以与现有的一些数据增强策略(如DIM、TIM、SIM等)相结合,得到一系列新的强大的对抗攻击。或者将这三种数据增强策略一起引入MI-FAGSM中,则可以得到一种更强大的对抗攻击,称为SI-TI-DIMI-FAGSM,其算法如下:

其中:
- $g_x,g_s,g_a$:3个中间变量
- $p$:DIM中的转换概率
- $W$:TIM中高斯核的大小
- $m$:SIM中的尺度拷贝数
- $T(x;p)$:表示$x$以概率$p$随机变换
- $g=W*g$:表示梯度$g$与核矩阵$W$卷积
- $S_j(x)=x/2^j$:表示尺度因子为$1/2^j$的输入图像$x$的尺度拷贝,$j$取值范围为$0\sim(m-1)$,$m$表示尺度拷贝数
实验
参数设置
- 最大扰动$\epsilon=16$
- 迭代次数$T=10$
- 步长$\alpha=\epsilon/T=1.6$
- 衰减因子$\mu=1.0$
- 对于数据增强策略:
- DIM转换概率设置为$0.5$
- TIM核矩阵设置为$15\times 15$的高斯核
- SIM的尺度拷贝数设置为$3$
实验结果
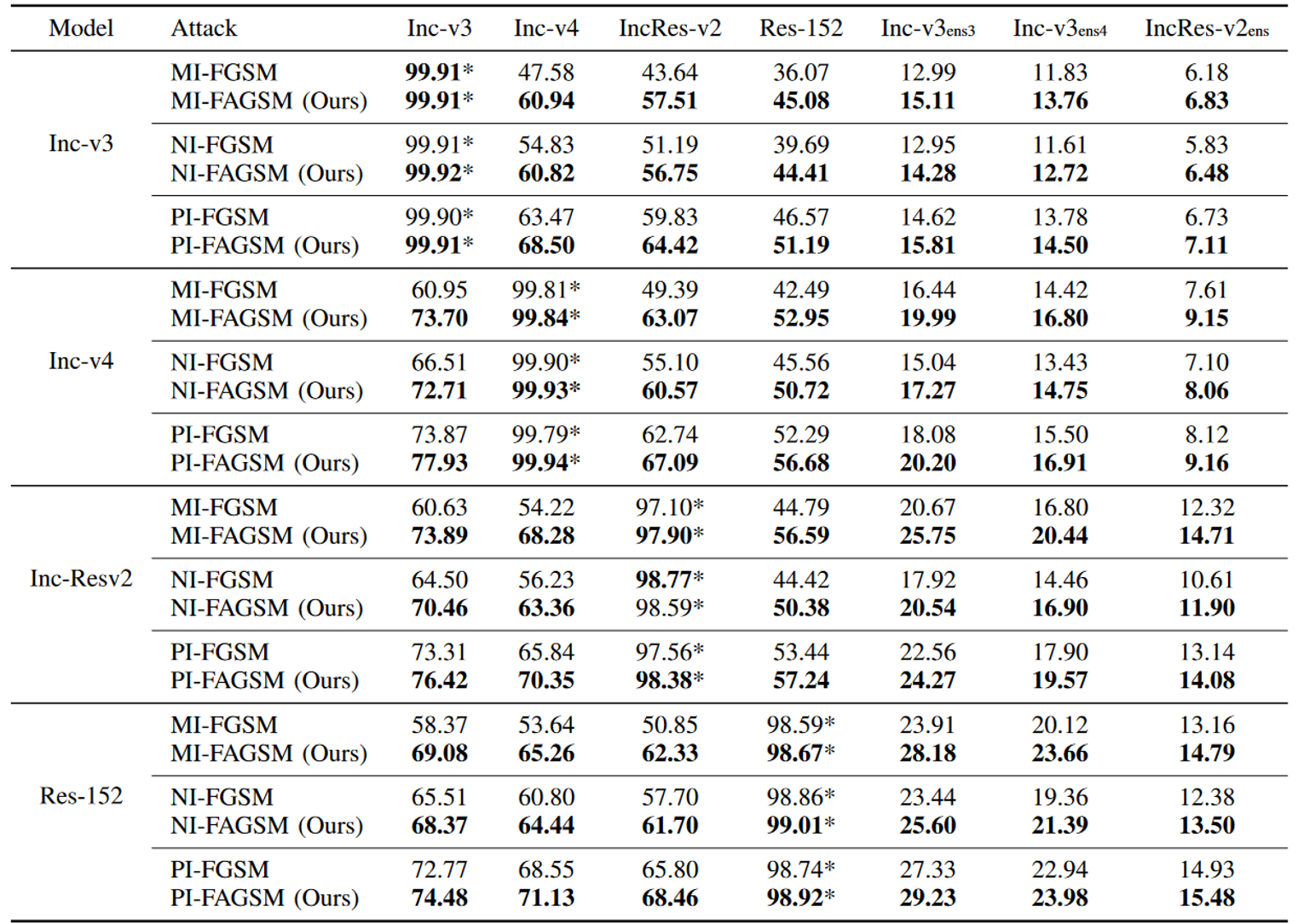
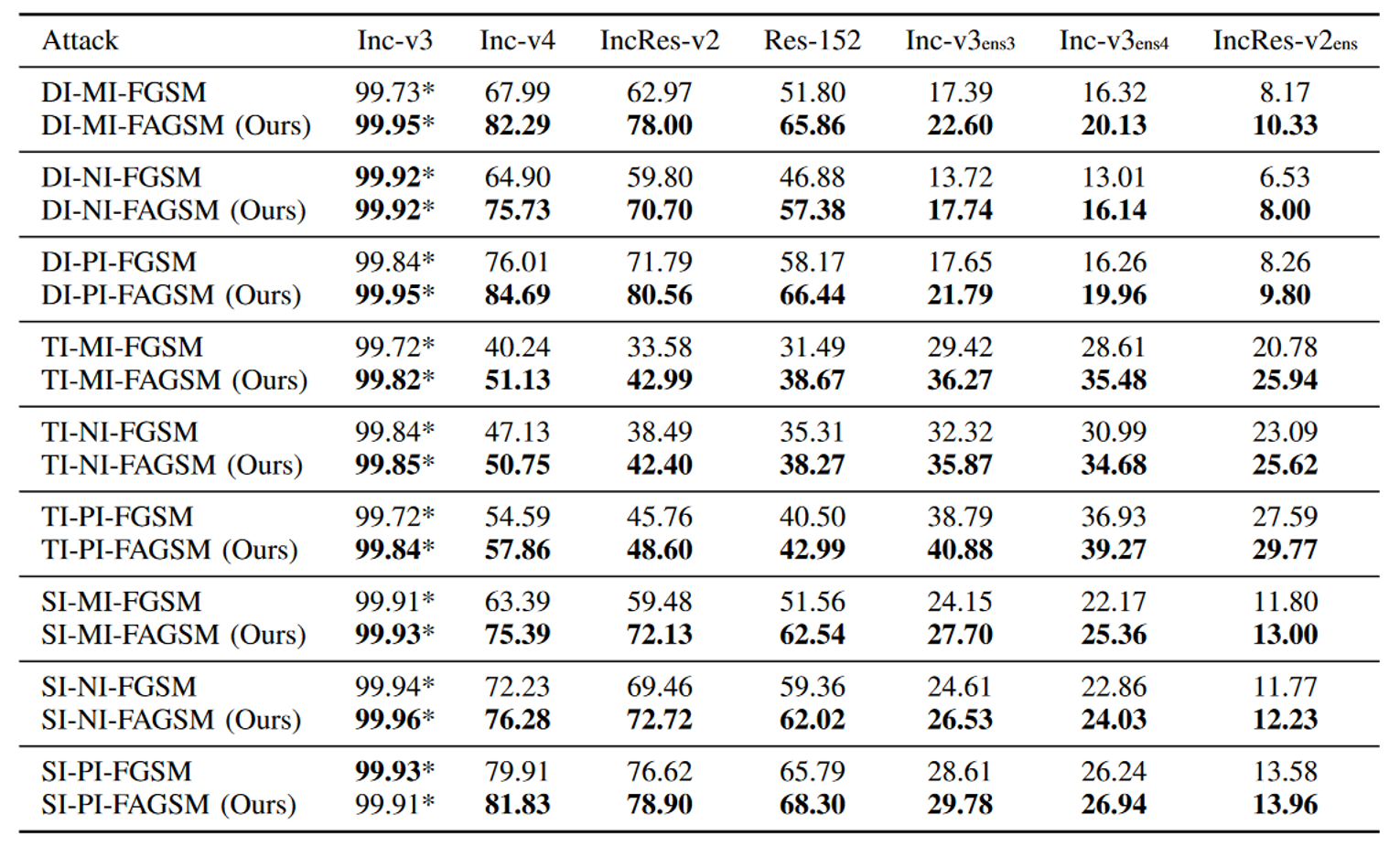
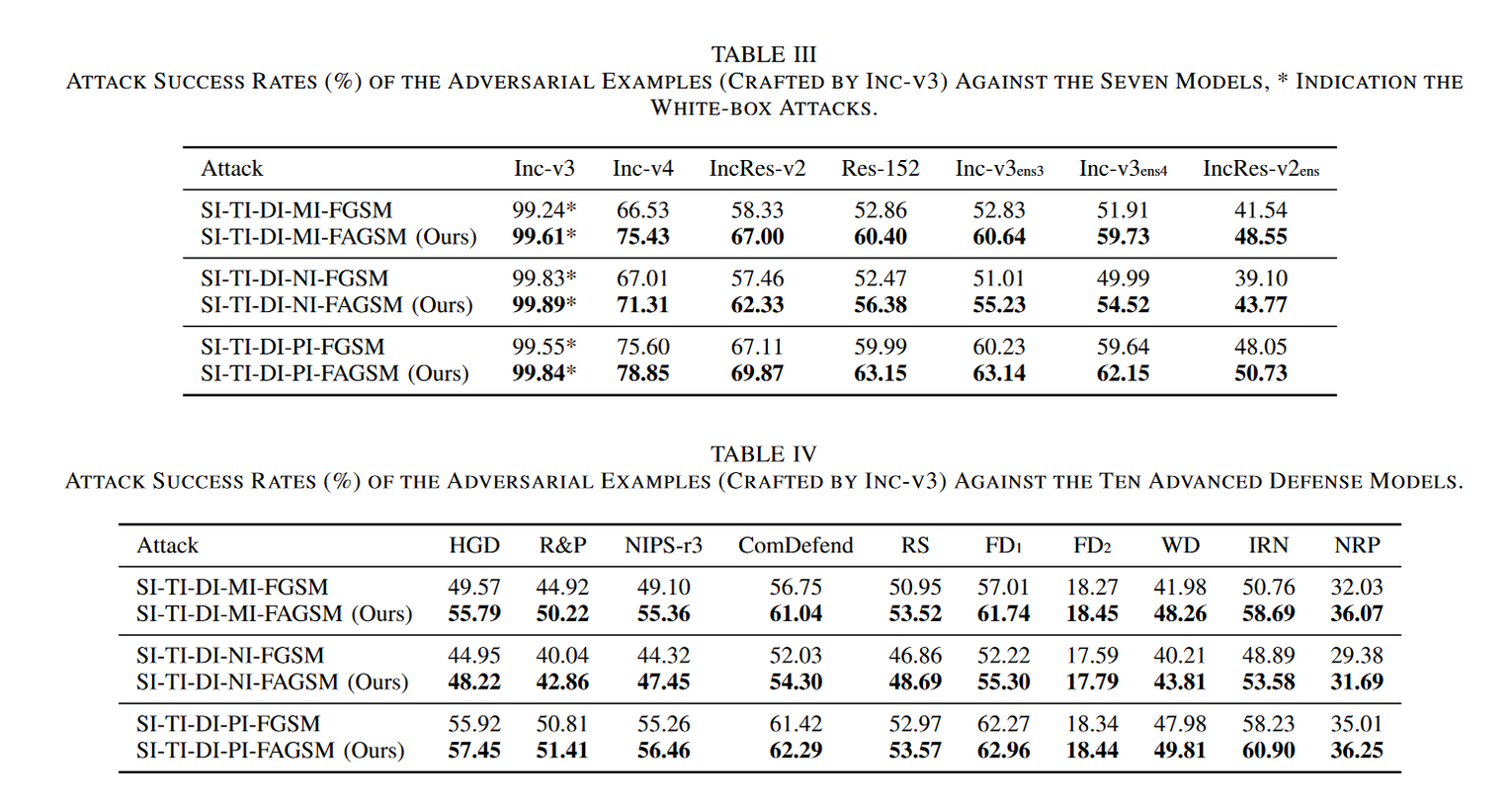
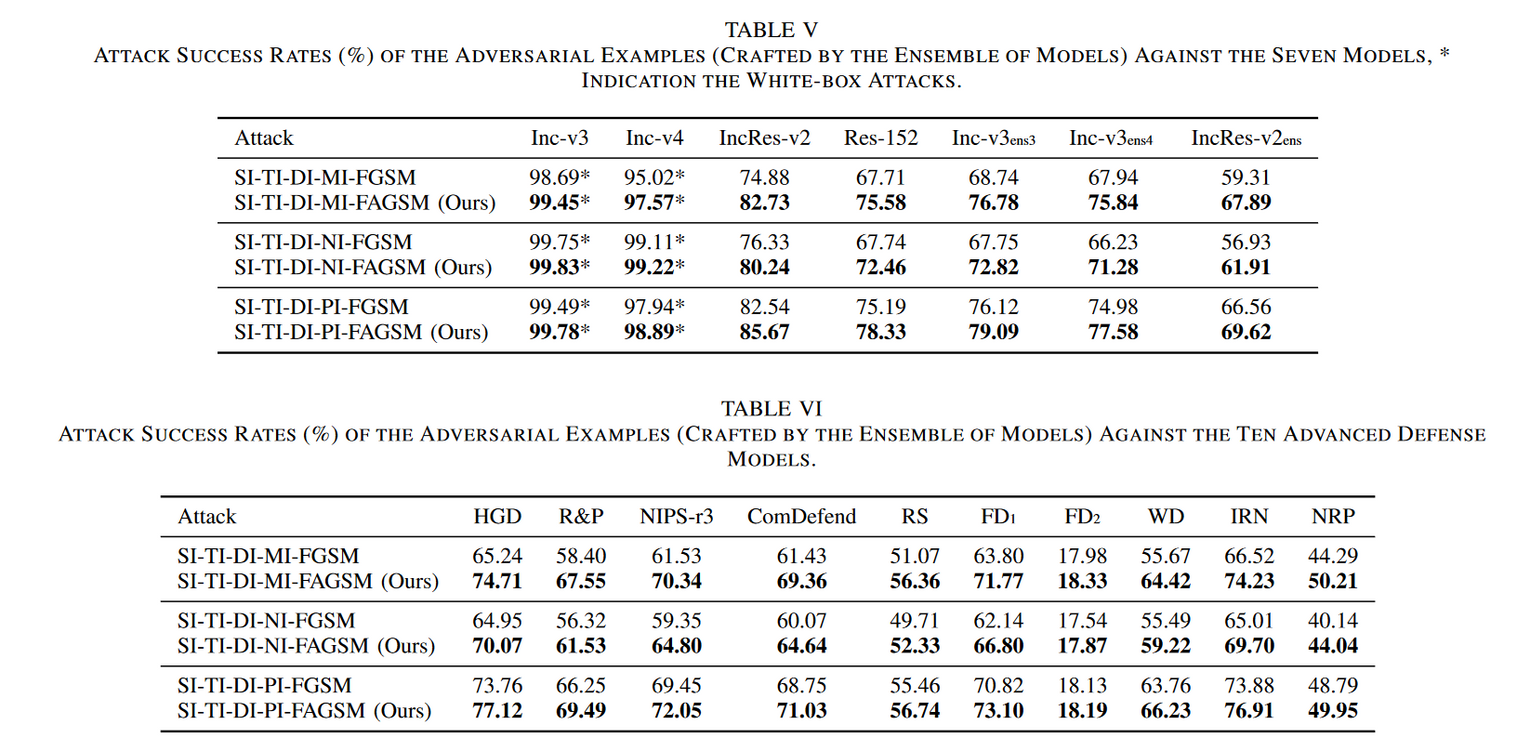
讨论
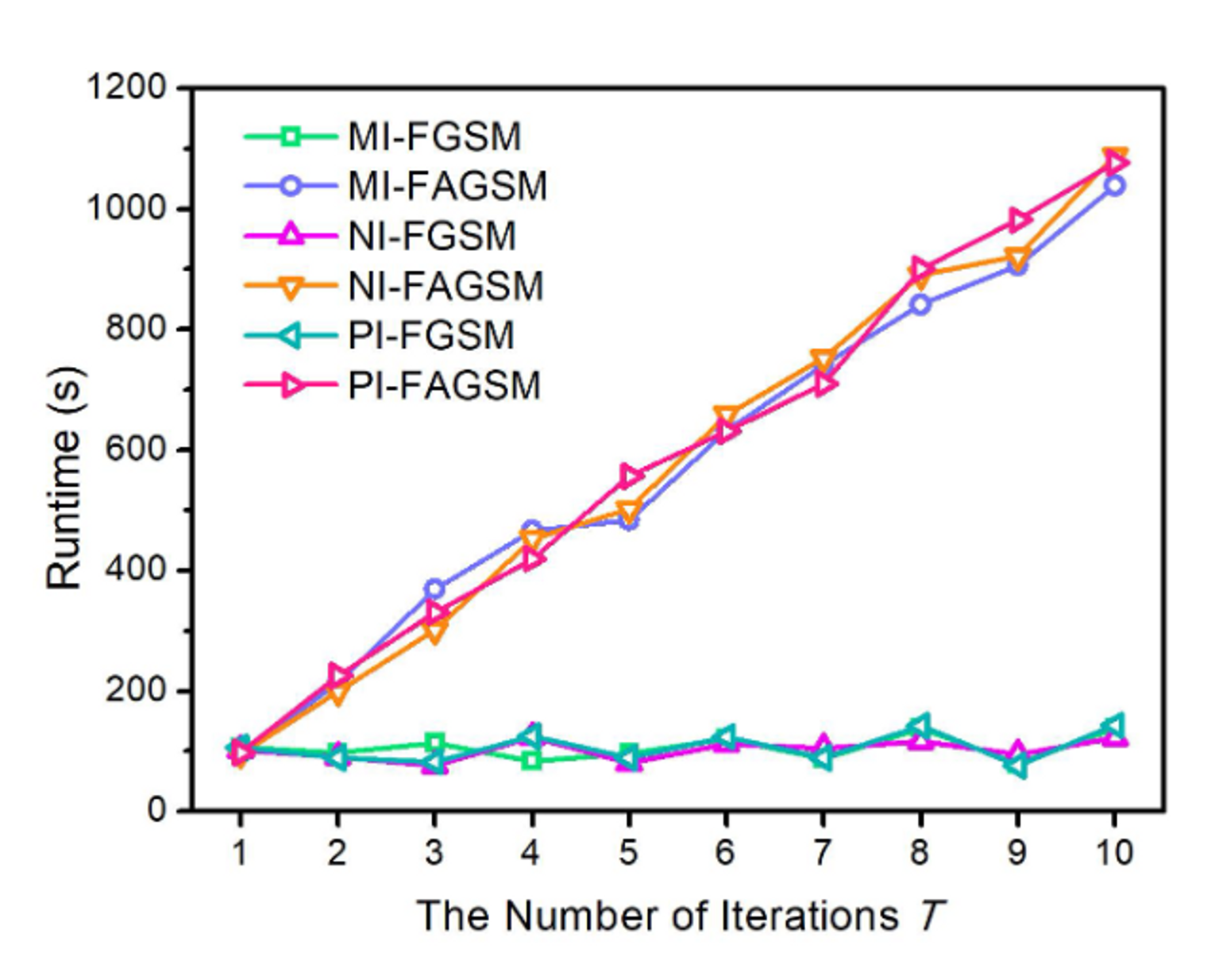
本方法在每次迭代中都会产生一系列的临时样本,用以计算损失函数关于所有临时样本的梯度。引入平均梯度项会增加方法的时间复杂度。







![[日常] v我50来点文子哥的保研经历](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/1728380966977.png)
![[计算机网络]可靠传输协议迭代设计-来跟👴握个手](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/v2-479a601f5f20bca19018dddb68c0d708_720w.jpg)
![[文献阅读]基于平均梯度的对抗攻击-I-FAGSM](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/image-20230813230657904.png)