[文献阅读]并行矩形翻转攻击PRFA-针对目标检测的基于查询的黑盒攻击
Information
日期:2022-01
关键词:Adversarial Attack
出处:CVPR 2022
简述
首先,目标检测在对对抗样本的脆弱性尚未得到充分的研究,特别是在黑盒攻击的实际场景下,攻击者只能访问被攻击模型返回的预测矩形框和top1分数的查询反馈。与针对图像分类的黑盒攻击相比,黑盒攻击对检测的挑战主要有两点。首先,即使一个边界框被成功攻击,也可能在被攻击边界框附近检测到另一个次优边界框。
其次,存在多个包围盒,导致攻击代价非常高。
为了应对这些挑战,本论文提出了一种基于随机搜索的并行矩形翻转攻击(PRFA)。
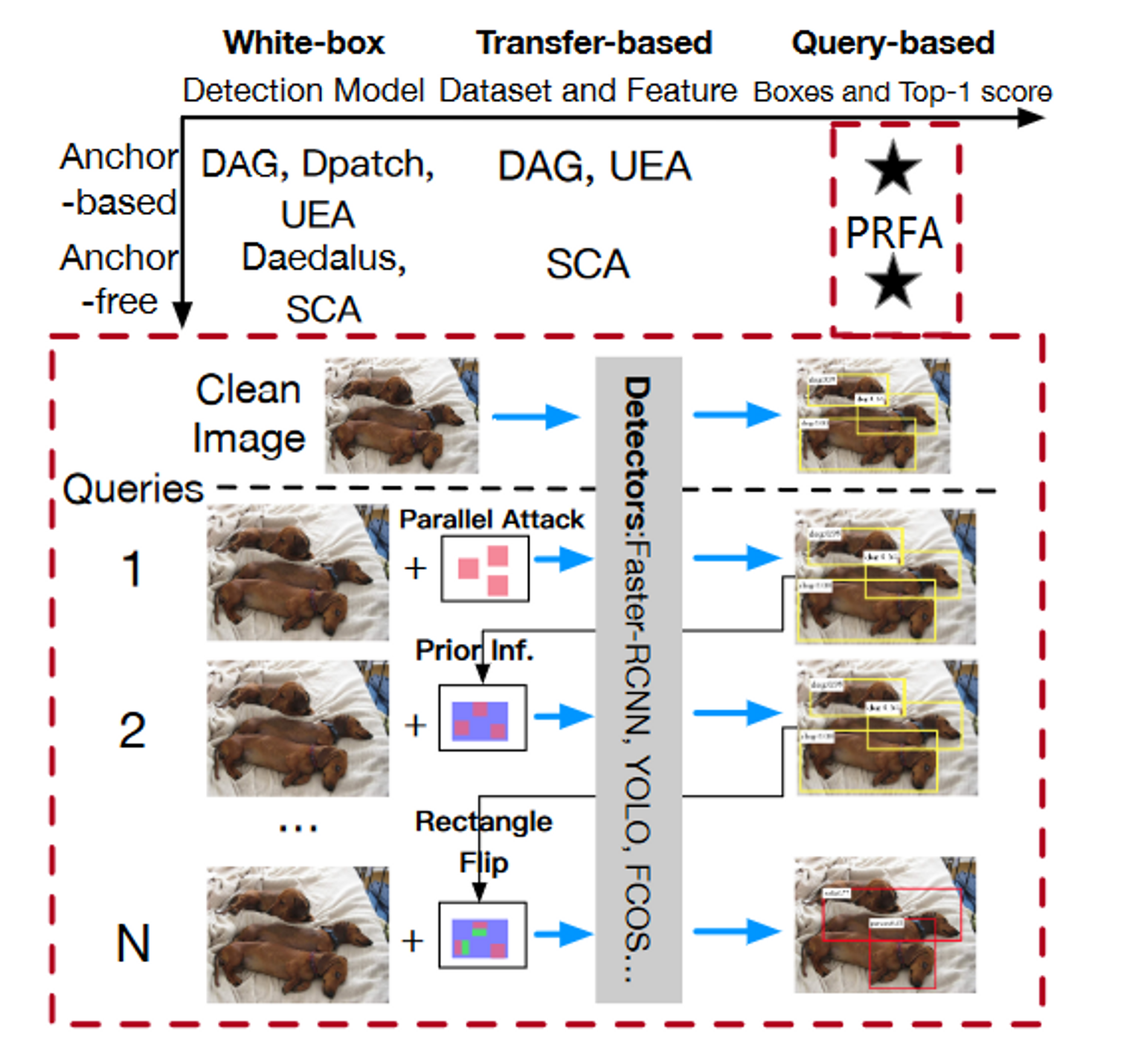
本论文:
在每个矩形块中产生扰动,以避免在攻击区域附近进行次优检测。
首先随机搜索一个矩形块,并生成符号沿垂直或水平方向反转的对抗性扰动,以呈现该攻击块中的任何检测,包括任何次优方案。
利用白盒攻击下对抗扰动主要集中在物体轮廓和临界点附近的特点,缩小攻击矩形的搜索空间,提高攻击效率。
开发了一种同时攻击多个矩形的并行机制,进一步加速了攻击过程。
相关工作
对象检测
主流的目标检测器大度基于深度神经网络DNNs,大致可以分为基于锚点和无锚点两类:
- 基于锚点的检测器将预定义的滑动窗口分为正样本或负样本,然后对预测框进行细化和分类。由于回归的形式不同,又可以细分为一阶段检测器和两阶段检测器。
- 无锚点的检测器舍弃了锚点,直接在对象中心预测边界框。由于无锚点的检测器不需要额外的参数调整,这类检测器得到了广泛的普及。
现有的针对目标检测任务的对抗攻击主要是白盒攻击。
图像分类的黑盒攻击
黑盒攻击包括基于传输的攻击和基于查询的攻击,攻击者通过访问模型的输出和修饰改性干净图像来获取对抗样本,采用可迁移的攻击策略,可以训练一个替代模型替代目标模型得到对抗梯度。
与图像分类不同,目标检测的优化问题是复杂的。假设$d$表示一幅图像的像素个数,每个候选区域由两个像素/坐标决定,目标检测的复杂度为$O(d^2)$,分类的复杂度为$O(d)$。检测器的输出为NMS后的预测框和top-1得分,使得对目标检测的黑盒攻击更像是一个介于基于得分和基于决策之间的中间设置。如何利用有限的信息和对检测器的查询实现有效的攻击是我们的研究重点。
并行矩形翻转攻击
界定问题
假设一副原始图像$x$有$M$个识别对象$O={o_1,o_2…,o_M}$,对于每一个对象$O_m$,$m=1,2,…,M$,用真实边界框$g_m$和类标$y_m\in{1,2,…,Y}$标记,其中$Y$为类的个数。目标检测器$f(x)\in R^{N\times(4+1)}$预测预测框$b_n$,$n=1,2,…,N$和top-1标签$c_n$,$n=1,2,…,N$,$N$个目标的得分$f_C$(对预测标签$C$进行softmax归一化后的概率)
生成对抗样本$\hat{x}\in[0,1]^d$,对于原始图像$x$,将其视为$l_p-norm$$=\epsilon$的对抗样本,即$||\hat{x}-x||_p<\epsilon$,目标是使所有预测框和真实框的IoU小于某个阈值或预测框的标签被错误分类,即$\forall n\in N,\ \forall m\in M,\ (IoU(b_n,g_m)<threshold)\vee(c_n≠y_m)$。其中,IoU分数是目标检测的标准性能指标,即$\mathsf{IoU}(a,b)=(a\cap b)/(a\cup b)$,检测任务的阈值设为$0.5$。
寻找$\hat{x}$的任务可以表述为求解下面的优化函数:
$\begin{split} \arg\min{\hat{ x}∈[0,1]^d} H(f (\hat{ x}), B, Y ) = \sum \limits{ n=1}^N\sum \limits ^ M {m=1} [IoU(b_n, g_m) · \mathbb{1}{f{c_n} ≥ζ} +\ λ · (f{cn} − \max \limits{ C ≠y_m} f_C ) · \mathbb{1}{f{c_n} <ζ} ],\ s.t. ||\hat{ x} − x||p ≤\epsilon , f{c_n} = f_C (\hat x, b_n)\end{split}$,(1)
其中:
- $\mathbb{1}$表示指示函数。如果$a$为帧,则$\mathbb{1}_a=1$,否则为0。
由于攻击满足等式中的一个条件。式(1)中,我们可以使用top1分数$f_{c_n}$作为判断优化公式之一。具体来说当top-1分数大于阈值$ζ$时,我们考虑降低相应预测框和真实值的IoU,当小于其时,我们优化top1分数。
本论文提出了一种基于类别的优化函数,将预测框和真实值在同一类别下进行优化,并将计算复杂度设置为$O(M*N/|Y|)$。由于检测数据集的类别太多,这样会大大提高一次查询的速度。$(N|y)$表示标号为$y$的对象的索引集合,即$(N|y)={i|c_i=y,i=1,2,…,N}$。新的优化函数$H$如下:
$\begin{split}\arg\min \limits{\hat{x}∈[ 0 , 1]^d} \sum \limits{y = 1}^Y\sum \limits^{ ( N | y )}{n = 1 }\sum \limits^{( M | y )}{m = 1}[ IoU( bn , gm) · \mathbb{1}{f{c_n}≥ζ} + \ λ · ( f{cn = y} ( \hat{x} , b_n )-\max\limits{ C≠ y} f_C ) · \mathbb{1}{f{c_n} < ζ}],\ s.t. || \hat{x}-x || p≤\epsilon,\ f{c_n} = f_C( \hat{ x} , b_n )\end{split}$ ,(2)
Priors&Objectness
本论文利用检测器的先验信息和白盒攻击下的先验观测来减少随机搜索空间。
虽然基于锚点和无锚点的模型在锚点上有着本质不同,但是都考虑了预测的客观性。Objectness(对象度?)本质上是一个对象在感兴趣区域中存在的概率的度量。如果对象度较高,则意味着图像窗口可能包含一个对象。我们攻击的是具有高对象度的区域而不是整幅图像。
此外本论文使用DAG和UEA方法来观察对抗扰动在不同模型上的分布。尽管攻击手段和目标模型不同,但扰动的分布都集中在目标的关键区域或轮廓上。
本论文使用预测框或先验信息计算一个高对象度的区域,并在该区域进行随即搜索。本论文通过随机抽样产生矩形扰动优化方程(2),该扰动在位置分布上与白盒比较接近。
三种计算对象度的方法:
- 基于锚点的先验(Mask-RCNN的分割结果)
- 无锚点的先验(关键点表示来自RepPoints)
- 预测框(探测器的输出)
并行攻击加速广度搜索
基于Square Attack,随着查询次数的增加,产生的对抗扰动逐渐聚集在对象周围。这一现象表明,在等式(2)的约束下,黑盒攻击方法可以在大量查询中发现易受攻击的像素,可以在一个查询中并行攻击多个位置,从而间接增加像素搜索次数,可以作为一种加速广度搜索的方法。
从理论上分析,每个查询$q$仅在一个随机位置生成对抗扰动$δ$并非最佳选择,假设优化后的检测器$f$为平滑度,且具有Lipschitz梯度,则存在常数$L$满足:
$f(x_{q+1})-f(x_q)≤\langle f’(x_q),δ\rangle+\frac L2||δ||^2$,(3)
随机梯度是无偏且方差有界的,其上界为常数$δ^2$。
SquareAttack方法满足:
$\frac1Q\sum\limits{q=0}^Q\mathbb{E}[||f’(x_q)||^2]\lesssim\frac{f(x_0)-\mathbb{E}[f(x{Q+1})]}{Q_\gamma}+\gamma L \sigma^2$,(4)
其中:
- $\gamma$为补偿,当$\gamma=\frac{1}{L+\sigma\sqrt{QL}}$时,收敛速度为$O(1/\sqrt{Q})$
- $\lesssim$意思是小且等于一个常数因子
式(4)意味着迭代次数$Q$足够大,随机搜索算法将收敛。
本论文提出了一种在图像上的并行随机搜索。每次迭代$q$可以随机采样搜索空间$D$中的$P$个位置,降低了梯度估计$\mathbb E[||g^P(x)-f’(x)||^2]≤(\frac{D-P}{D-1})\frac{\sigma^2}{P}$的方差,加速了算法的收敛,此时收敛性可以表示为:
$\frac1Q\sum\limits^Q_{q=0}\mathbb E[||f’(x_q)||^2]\lesssim\frac L Q+\frac{\sqrt{L}\sigma}{\sqrt{Q}P}$,(5)
式(5)中的查询$Q$对算法收敛性的影响仍然比并行攻击次数$P$更显著,收敛速度比式(4)快$O(1/\sqrt QP)$。
由于查询的前期迭代次数较少,样本数$P$最大,随着迭代次数的增加,逐渐减小$P$的值直到$1$。
针对深度搜索的矩形翻转攻击
一般而言,检测数据集中用矩形框标记的对象具有固定的尺寸和尺度。检测器使用固定比例的预定义锚点是一种典型的先验。
例如,Faster-RCNN采用1:1、1:2、2:1的锚点设置,YOLO通过k-mwans聚类从训练集中学习不同的锚点
实验观察可知,给定一个边界框内的一个区域,相对于用相似的噪声进行扰动,用不同的噪声对不同的子区域进行扰动更有可能导致该区域被分别检测到不同的边界框。
此外,如图3所示,矩形框往往覆盖了一个物体的局部区域,水平或垂直反转符号可以提高扰动的多样性。因此,该区域更容易被误检为不同的包围框,导致该对象上的原始包围框发生变化。
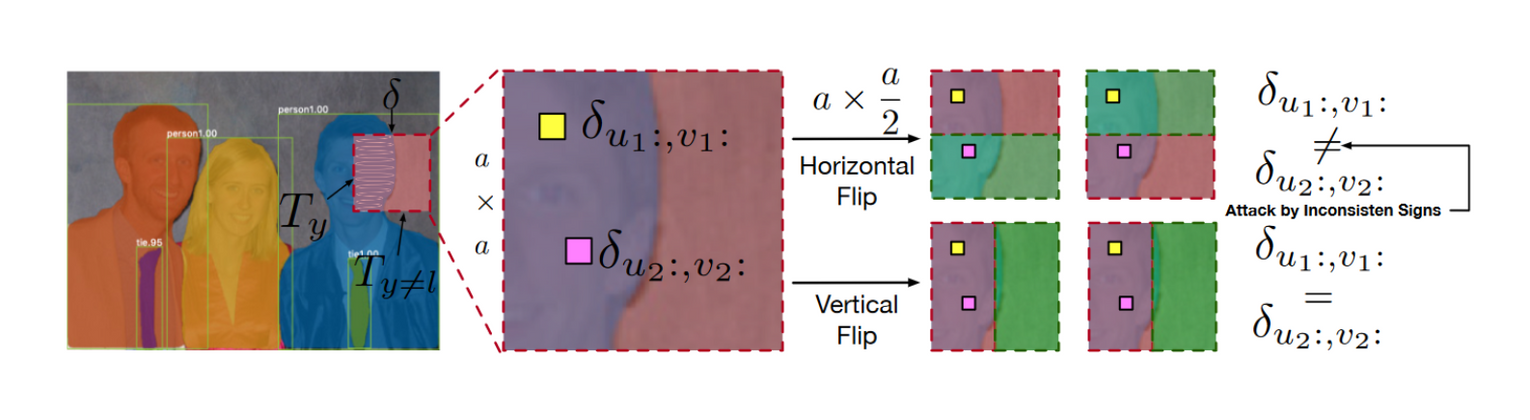
给定一个$\epsilon$约束的初始矩形$\delta\in\mathbb{R}^{a\times a}$和一个卷积滤波器$w\in\mathbb{R}^{k\times k}$。令$z=F((xp+\delta)w)$表示CNN的输出来更新$\delta$,其中$F$表示激活函数,$x_p$表示原始补丁(干净补丁)。$(m,n)$表示对抗补丁$\hat{x}p$的坐标。将$(m,n)$划分为$|Y|+1$个团${T_i}*{i=0}^{|Y|+1}$,且$(u,v )\in T_i$表示第$i$个团中某一点的坐标。$\alpha$为大于0的常数。$z$的最大变化$l∞-norm$表示为:
$\begin{split}| | z | |∞= \max\limits{ m,n }| zm,n |\ = \max\limits{ m,n }| F ( \sum\limits^k{i , j = 1} ( x_p + δ){m-\lfloor \frac s 2 \rfloor + i,n-\lfloor \frac s 2 \rfloor + j} · w{i,j} ) |\≤\max\limits{ m,n} | F ( \sum\limits ^k{ i , j = 1}δ{m-\lfloor\frac s2\rfloor + i , n-\lfloor \frac s2 \rfloor + j} · w_{i , j}) + α |\end{split}$,(6)
对于目标检测中的对抗攻击,一个补丁中包含的目标的正确标签$y$的最大变化分量应该小于其他类的最大变化分量。补丁$\hat{x}_p$中的优化函数$H$可表示为:
$\begin{split}\min\limits\delta H\approx\min\limits\delta[\sum\limits{(u,v)\in T_y}^{T_y}max|F(\sum\limits{i,j=1}^k\delta{u:,v:}\cdot w{i,j})+\alphay|\-max\sum\limits{l≠y}^{|Y|}[\sum\limits{(u,v)\in T_i}^{T_i}max|F(\sum\limits^k{i,j=1}\deltal\cdot w{i,j})+\alpha_l|]]\end{split}$,(7)
其中$\delta{u:,v:}$是式(6)中的简写。同时,由于若两个点位于同一个框区,属于同一个团,那么他们的扰动应该是相同的,即$(u_1,v_1)\in T_l$$(u_2,v_2)\in T_l$,那么$\delta{u1:,v_1:}=\delta{u_2:,v_2:}$,因而使用近似。
当扰动在每个点上符号正确且一致时,团$T_y$的变化值最大。由于我们攻击的关键区域包含对象$y$,因此标记位$T_y$的团占据主导地位,使得式(1)最小化。式(7)中,我们可以最小化上项的界限。补丁中属于同一框区的点在空间位置(value接近)和语义特征(性质接近)上高度相似。因此,如果扰动项的符号能够改变一个点的语义特征,那么对于其他概率较大的点也是有效的。因此可以通过翻转符号来产生一个矩形扰动,使得同一个团中的点是不一致的,并将他们推到不同的分类边界,由此最小化方程。
对抗样本的生成
- 利用Prior&Objectness章节中的方法获取中检测器的先验信息,以计算高对象度的区域,确定临界点进行随机搜索。
- 根据动态调度算法设定了方形扰动的边长$a$和并行点数$P$。
- 首先为每次迭代生成边长$a$的方形扰动,接着将方形扰动的一半($a*a/2$的矩形)的符号垂直或水平翻转。
- 通过式(2)计算分数,若当前得分大于最优分数,则更新对抗扰动。
实验
实验设置
检测数据集
MS-COCO的前100张图像作为黑盒攻击的干净图像,这些样本包含丰富的对象实例,如小对象或稠密对象。
评价标准AP
不同召回率下的平均检测准确率,我们通常以特定类别的方式(如平均AP、mAP)对其进行评估。我们采用MS-COCO提供的评价标准,例如:
- $mAP$(在0.5~0.95之间的多个IoU阈值上取平均值)
- $mAP_{50}$(IoU=0.5的平均AP)
- $mAP_{75}$(IoU=0.75的平均AP)
- $mAP_5$(面积<322)
- $mAP_M$(322<面积<962)
- $mAP_L$(面积>962)
一个有效的黑盒攻击意味着一个小的$mAP$。在算法效率方面,我们使用$AQ$(平均查询)来评估算法的收敛性。我们希望尽可能减少查询次数。
目标模型
选取4个具有代表性的检测器作为目标模型:
基于锚:
- 以ResNet50网络为骨架的两级检测器Faster-RCNN
- DarkNet53为骨架的YOLOv3模型
无锚:
- 以ResNet50为骨架的FCOS
- 可以自适应选择正负样本的检测器ATSS(可以消除基于锚顶啊和无锚点算法的性能差异)
参数设置
给定大小$wh$的图像,长度为$a$的方形的长度为$\sqrt{ew*h}$,$e\in [0,1]$
- $e$$=0.05$,在查询$q\in{20,100,400,1000,2000,4000,8000}$时$e$减半
- 初始阶段并行$P=4$,在查询$q\in{20,100,1000,2000}$时减半
- 式(2)中$ζ=0.90$,$\epsilon=0.50$
- IoU阈值为$0.50$
消融实验
通过攻击性能(如$mAP$的降低)和查询来评估。
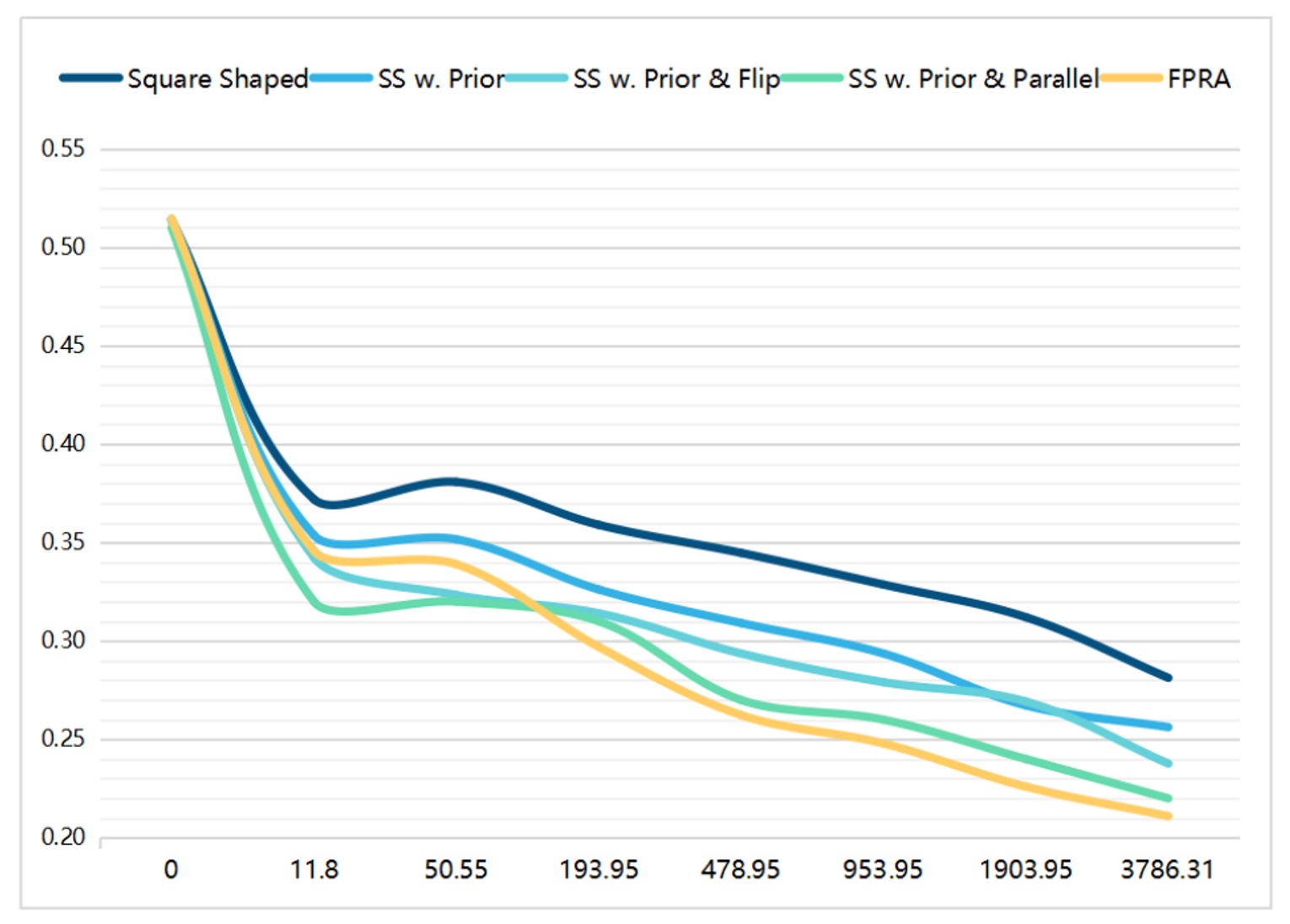

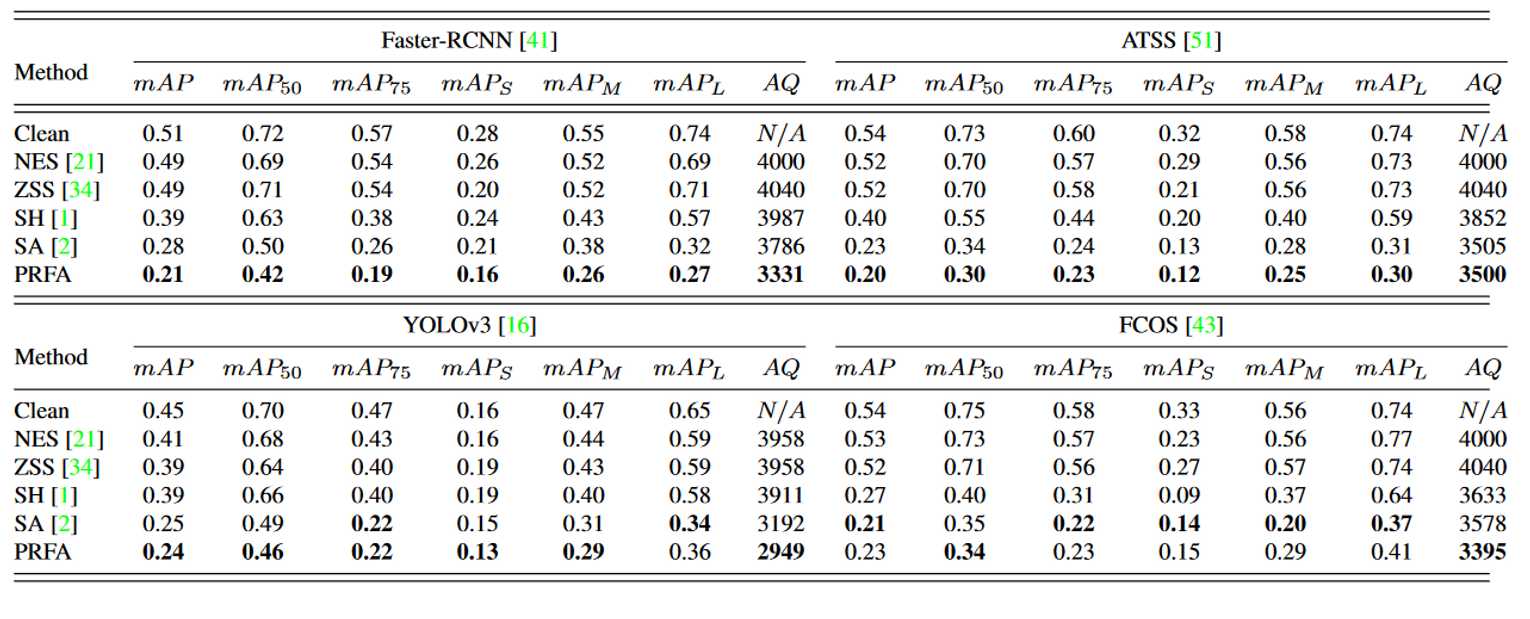
黑盒攻击的可迁移性
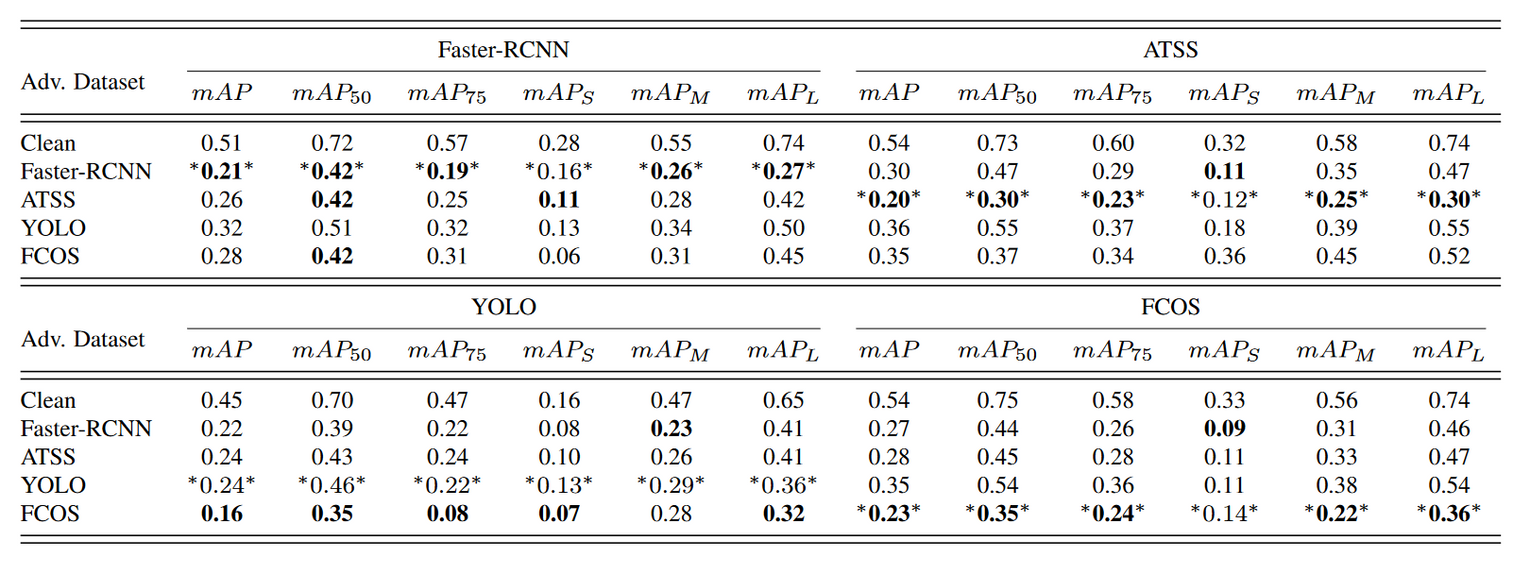
可知,Faster-RCNN、ATSS和FCOS三个模型的攻击效果是稳健的,因为其能够抵御来自其他数据集的攻击。
其中,最稳健的方法是ATSS,在其他数据集上达到了至少0.30$mAP$的效果。
YOLO是最容易被攻击的模型,其他模型生成的对抗样本可以有效攻击他,甚至超过自身生成的对抗样本。







![[日常] v我50来点文子哥的保研经历](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/1728380966977.png)
![[计算机网络]可靠传输协议迭代设计-来跟👴握个手](https://image-host-mooliht.oss-cn-beijing.aliyuncs.com/img/v2-479a601f5f20bca19018dddb68c0d708_720w.jpg)